Золотой билет. P, NP и границы возможного - Лэнс Фортноу Страница 39

Реальность для Тома определяется тем, что он видит. Он смотрит последний иннинг – а значит, в его мире еще никто не победил. Матч продолжается; и пока не закончится последний розыгрыш, он так и будет находиться в промежуточном состоянии между победой «Ред Сокс» и их поражением.

Сьюзен – ярый фанат «Янкиз». Она тоже записала игру и теперь, как и Том, смотрит ее в оффлайн-режиме и гадает, заработает ли Хаммер победное очко. Для Сьюзен, как и для Тома, результат игры еще не определен; он случаен – ровно до того момента, пока Сьюзен не услышала финальный свисток.

Том и Сьюзен одновременно наблюдают разные случайные события, находясь в 200 милях друг от друга. И все же результат они увидят совершенно одинаковый. И для Тома, и для Сьюзен Хаммер либо заработает победное очко, либо не заработает. Не может быть такого, чтобы в мире Тома Хаммер заработал очко, а в мире Сьюзен – нет. Исход игры никто из зрителей пока не знает, однако оба уверены, что в конце увидят на табло один и тот же счет. Результаты событий, отражаемых на экранах телевизоров Тома и Сьюзен, каким-то загадочным образом связаны друг с другом.

Вы спросите, причем здесь квантовые вычисления? В классических цифровых компьютерах основной логической единицей является бит, или двоичная цифра (от англ. bit – binary digit). Каждый бит может принимать ровно два значения, например – истина и ложь, или победа и поражение. Базовый элемент квантовых компьютеров – это кубит, или квантовый бит (от англ. qubit – quantum bit). В отличие от бита, который всегда принимает одно из двух пограничных значений, кубит может находиться в некотором промежуточном состоянии, называемом суперпозицией.

Записанные на телевизор бейсбольные игры – это, конечно, не кубиты, однако с кубитами у них имеется много общего. Пока игра идет, она находится в неопределенном, промежуточном состоянии, и это продолжается вплоть до финального свистка. Затем Том наблюдает окончание игры, и тут уже всякая неопределенность исчезает, поскольку становится ясно, кто выиграл, а кто проиграл. С кубитом дело обстоит аналогичным образом: как только за ним начинают наблюдать, он покидает свое промежуточное состояние и принимает одно из двух пограничных значений, превращаясь в самый обыкновенный бит.

Квантовые биты могут быть определенным образом связаны, или запутаны, – например, так, что при каждом измерении они будут приходить в одно и то же состояние. Нечто подобное происходит и при просмотре записанных на телевизор бейсбольных игр.

Впрочем, на этом совпадения кончаются. В общем случае связи между кубитами намного тоньше и сложней. Управляя запутанными системами кубитов, можно организовывать целые вычислительные процессы.

Состояние бейсбольного матча «ходит» вдоль одной оси: это просто вероятность того или иного исхода.

Рис. 9.1. Бостонская команда

Звездочкой обозначена тридцатипроцентная вероятность победы Бостона. Пока Том смотрит матч, звездочка перемещается; в зависимости от исхода игры она попадет либо в самую левую точку, либо в самую правую.

Состояния кубита образуют окружность с центром в точке пересечения осей «Истина» и «Ложь».

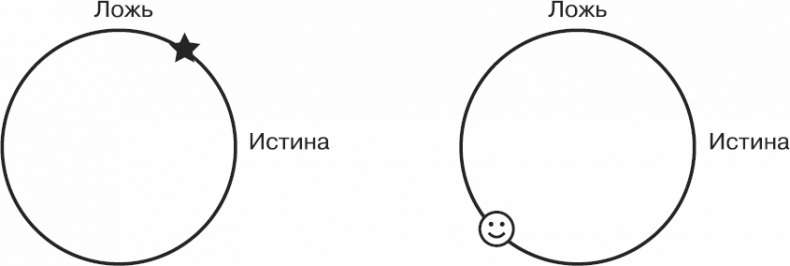
Рис. 9.2. Кубиты

В данном случае звездочка перемещается по двумерной траектории. На рис. 9.2 ее текущие координаты – 0,55 по «Истине» и 0,84 по «Лжи». Координаты вполне могут быть и отрицательными: к примеру, смайлик находится в точке (-0,71; -0,71). Квантовые компьютеры вращают и переворачивают эти окружности и таким образом управляют состояниями кубитов.

Одному кубиту соответствует окружность на плоскости. Двум кубитам требуется четырехмерная окружность; нарисовать ее здесь или даже просто представить в уме было бы довольно затруднительно. В системе из тридцати кубитов размерность пространства будет более триллиона.

Все это наводит на мысль использовать квантовые компьютеры для решения NP-задач. Допустим, нам нужно найти клику размера 50 среди 20000 жителей Королевства. Имея около 500 кубитов, мы сможем воспроизвести сразу все группы размера 50, которые будут обрабатываться параллельно; чтобы отметить клику, квантовый компьютер выполнит определенную последовательность вращений и переворотов.

В результате система придет в квантовое состояние, представляющее собой совокупность приблизительно из 3 × 10¹⁵⁰ (т. е. 3 и 150 нулей) групп, часть которых отмечены как клики. Если мы научимся эффективно «вытаскивать» из квантовых состояний информацию о кликах, то получим быстрый квантовый алгоритм для поиска клики, а также для всех остальных NP-полных задач. Считывая квантовое состояние системы (т. е., в некотором роде, наблюдая за окончанием игры), мы видим лишь один исход, в данном случае – одну группу жителей; маловероятно, что именно эта группа окажется кликой.

Нам нужно научиться как-то выделять искомые клики, чтобы при считывании квантового состояния они попадались нам с большей вероятностью. Сделать это можно при помощи квантовых манипуляций с кубитами. Правда, при грубом подходе манипуляций потребуется столько же, сколько и групп, т. е. примерно 3 × 10¹⁵⁰, и все преимущества квантовых вычислений будут сведены на нет. В 1996 году сотрудник Лабораторий Белла в Нью-Джерси Лов Гровер разработал «умный» квантовый алгоритм, который мог обнаружить клику в Королевстве «всего» за 2 × 10⁷⁵ квантовых шагов. Однако даже при скорости триллион операций в секунду на это ушло бы в пять раз больше времени, чем живет наша вселенная.

Уже доказано, что при решении NP-полных задач на квантовом компьютере алгоритм Гровера в общем случае дает наилучший результат, поэтому квантовые алгоритмы вряд ли позволят приравнять классы P и NP. Если физики когда-нибудь и построят полноценные квантовые компьютеры, самые трудные проблемы все равно окажутся им не по зубам.

Это, конечно, не означает, что от квантовых компьютеров не будет никакого толку. С их помощью мы сможем эффективно эмулировать нетривиальный жизненный цикл различных наносистем и постепенно приоткроем завесу над тайнами вселенной. А еще квантовые компьютеры помогут нам решить некоторые NP-задачи, с которыми обычные компьютеры за разумное время не справляются.

В 1994 году другой сотрудник Лабораторий Белла, Питер Шор, придумал, как на квантовом компьютере можно быстро выполнять факторизацию, т. е. раскладывать число на простые множители (к примеру, для числа 16461679220973794359 тут же выяснилось бы, что 16461679220973794359 = 5754853343 × 2860486313). При наличии мощного квантового компьютера алгоритм Шора спокойно работал бы с числами из сотен и даже тысяч знаков. Для поиска делителей алгоритм строит алгебраические конструкции, с которыми квантовые компьютеры справились бы очень легко. Современным машинам такая задача не под силу, а вот квантовые могли бы эффективно факторизовывать сколь угодно большие числа. К сожалению, хорошие алгебраические конструкции для NP-полных задач пока не придумали, поэтому для них алгоритм Шора работать не будет.