Стратегии решения математических задач. Различные подходы к типовым задачам - Альфред Позаментье Страница 4
Стратегии решения математических задач. Различные подходы к типовым задачам - Альфред Позаментье читать онлайн бесплатно
Ознакомительный фрагмент

Можно также объединить решение более простой задачи с визуальным представлением (схематичным изображением), организацией данных и распознаванием закономерности. Начнем с рассмотрения одного человека, представленного одной точкой. Здесь, очевидно, мы имеем ноль рукопожатий. Затем увеличим количество людей до двух, представленных двумя точками. В этом случае у нас будет одно рукопожатие. Увеличим количество людей до трех. Теперь получим три рукопожатия. Продолжим увеличивать количество людей до четырех, пяти и т. д.
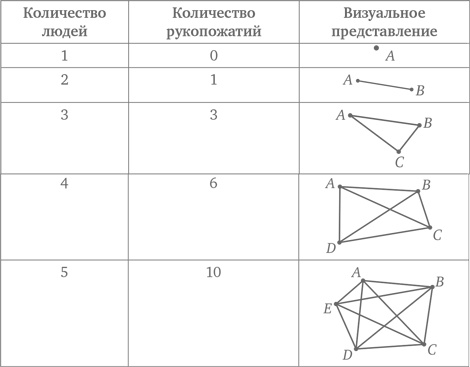
Задача становится геометрической, где ответом является количество сторон и диагоналей «n-угольника». Таким образом, для 10 человек мы получаем 10-угольник, у которого число сторон n = 10. Для определения количества диагоналей можно использовать формулу:
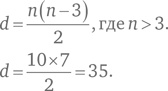
Итак, количество рукопожатий = 10 + 35 = 45.
Конечно, некоторые читатели уже видят, что эту задачу можно легко решить с помощью комбинаторной формулы для определения числа сочетаний из 10 элементов, которые берутся по два за раз.
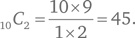
Впрочем, это решение, хотя оно эффективно, кратко и правильно, практически не требует математического мышления (если не считать применения формулы) и обходится без какого-либо подхода к решению задач. Несмотря на то, что такое решение имеет право на существование, только другие решения позволяют продемонстрировать различные стратегии, а именно с этой целью мы и привели данную задачу.
Мы предполагаем, что вы будете читать эту книгу, решать задачи и, таким образом, знакомиться со стратегиями. Это позволит вам составить собственный набор стратегий решения задач, который станет базовым в решении ваших задач. У тех, для кого решение задач является новым делом, мы надеемся пробудить интерес и подтолкнуть к дальнейшему изучению этого полезного аспекта математики. Те же, кто уже интересуется критическим мышлением и решением задач, найдут здесь новые, занятные и нестандартные задачи, способные захватить внимание. Приятного вам чтения!
Логическое рассуждение
Выделение целой главы такой стратегии, как логическое рассуждение, может показаться излишним. В самом деле, без логического мышления, хотя оно и используется для решения задач, немыслимо применение ни одной стратегии. Для многих людей решение задач является практически синонимом логического рассуждения, или логического мышления. Так зачем же тогда нужна эта глава, и зачем вообще выделять эту стратегию?
В повседневной жизни мы прибегаем к логическому рассуждению, когда спорим о чем-нибудь с кем-то. И это понятно — во время спора мы рассчитываем на то, что определенные доводы будут вызывать конкретную реакцию. На работе мы с помощью логической цепочки доводов добиваемся изменения того или иного производственного процесса. Мы логически выстраиваем цепочку утверждений в надежде на получение желаемого вывода. В суде, например, адвокаты используют логическое рассуждение, чтобы представить дело в нужном им свете. Если мы назначаем кому-то встречу через два дня, а сегодня суббота, то логика подсказывает нам, что встреча должна состояться в понедельник.
В математике некоторые задачи решаются без использования каких-либо других стратегий, включая и представленные в этой книге. Они требуют строгих рассуждений и формулирования утверждений, которые логически вытекают одно из другого. Возьмем, например, такую задачу.
Найдите все пары простых чисел, сумма которых равна 741.
Многие наверняка составят перечень всех простых чисел меньше 741 и будут подбирать к ним пару, дающую в сумме 741. Вместе с тем работу можно упростить с помощью логического рассуждения. Если сумма двух чисел является нечетным числом, то одно из слагаемых должно быть нечетным, а другое — четным. Как известно, существует только одно четное простое число — 2. Значит, другим числом должно быть 739 (а 739 — это простое число). Таким образом, мы нашли все пары, которые удовлетворяют условиям задачи.
Рассмотрим еще одну задачу, которая решается путем логического рассуждения.
Палиндромическим называют такое число, которое читается одинаково слева направо и справа налево. Примерами трехзначного и четырехзначного палиндромов являются 373 и 8668. Мария выписала все трехзначные палиндромы на листочки бумаги и положила их в большую коробку. Мигель выписал все четырехзначные палиндромы и положил листочки с числами в ту же коробку. Учитель тщательно перемешал листочки и попросил Лору взять один из них не глядя. Какова вероятность того, что она вытащит четырехзначный палиндром?
Один из способов решения — выписать все трехзначные и четырехзначные палиндромы, пересчитать их и определить искомую вероятность. Такой подход дает надежный результат, хотя и требует времени. Вместе с тем логическое рассуждение позволяет упростить работу. В качестве примера трехзначного палиндрома можно взять 373. Чтобы превратить его в четырехзначный палиндром, нужно всего лишь удвоить среднюю цифру — 3773. Повторяя это действие, мы можем превратить каждый трехзначный палиндром в четырехзначный. Таким образом, количество четырехзначных палиндромов равно количеству трехзначных, и вероятность выбора листочка с четырехзначным палиндромом составляет один из двух, или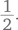
Покажем еще на одном примере, насколько просто решаются задачи путем логического рассуждения.
На прилавке цветочного магазина стоят три коробки с декоративными бантиками для украшения подарочной упаковки. Марк решил пометить коробки ярлыками с надписями «Красные», «Белые» и «Разноцветные» (красно-белые). К сожалению, он наклеил эти ярлыки неправильно. Поскольку коробки стоят высоко, Марк не может заглядывать в них. Он знает, что коробки помечены неправильно, и хочет достать бантик из одной из них. Из какой коробки ему нужно достать бантик, чтобы пометить коробки правильно?
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии