Тайны чисел. Математическая одиссея - Маркус Дю Сотой Страница 4
Тайны чисел. Математическая одиссея - Маркус Дю Сотой читать онлайн бесплатно
Ознакомительный фрагмент
Для математика самая любопытная особенность состоит в выборе числа: ведь 17 – простое число. Является ли всего-навсего совпадением то, что цикады проводят под землей простое число лет? По-видимому, нет. Есть вид цикад, который скрывается под землей 13 лет, а также другой вид, с 7-летним циклом. Все это простые числа. Довольно удивительно, что если цикада с 17-летним циклом появляется слишком рано, то сдвиг уже будет не на год, а обычно на 4 года, тем самым происходит переключение на 13-летний цикл. Кажется, в простых числах есть что-то, способствующее всем этим разновидностям цикад. Но что же это?
Хотя ученые и не пришли к окончательным выводам, имеется математическая теория, которая объясняет склонность цикад к простым числам. Сперва несколько фактов. В лесу может быть только один выводок цикад, так что объяснение не касается совместного использования ресурсов несколькими выводками. Почти каждый год где-либо в Соединенных Штатах появляется выводок цикад с циклом, составляющим простое число лет. Но в 2009 и 2010 гг. цикад не было. Напротив, в 2011 г. на юго-востоке США было массивное нашествие цикад с 13-летним циклом. (Кстати, 2011 является простым числом, но все же я не думаю, что цикады настолько умны.)
Лучшая на сегодняшний день теория простых чисел, лежащих в основе цикла цикад, исходит из возможного существования хищника, который также периодически появляется в лесу. Появление хищника приходится на время нашествия цикад, и он пирует, поедая насекомых. Но тут в дело вступает естественный отбор, потому что цикады, которые регулируют свою жизнь, исходя из цикла, составляющего простое число лет, будут значительно реже сталкиваться с хищниками, чем цикады с жизненным циклом, не представляющим простое число.
Предположим, например, что хищники появляются каждые 6 лет. Цикады с 7-летним циклом будут совпадать с хищниками лишь раз в 42 года. В отличие от них цикады с 8-летним циклом будут появляться одновременно с хищниками каждые 24 года; у цикад же с 9-летним циклом совпадение будет еще чаще – каждые 18 лет.

Рис. 1.02. Взаимодействие на протяжении 100 лет между популяциями цикад с 7-летним жизненным циклом и хищников с 6-летним
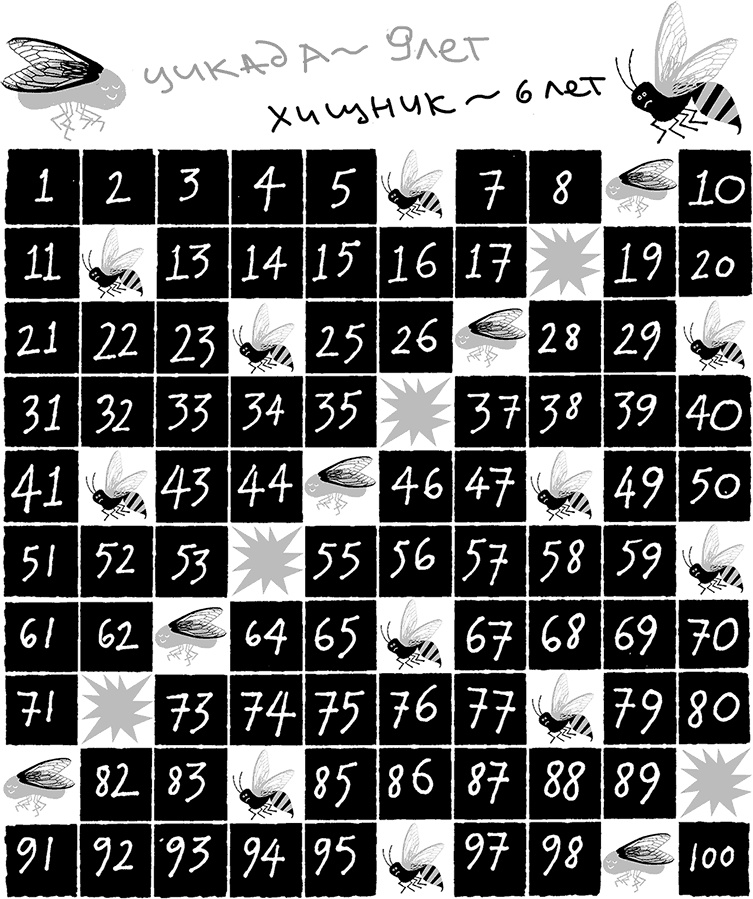
Рис. 1.03. Взаимодействие на протяжении 100 лет между популяциями цикад с 9-летним жизненным циклом и хищников с 6-летним
В лесах Северной Америки было, по-видимому, настоящее соревнование, чтобы найти наибольшее простое число. Цикады настолько преуспели в этом, что хищники либо вымерли, либо переселились, оставив цикад с их странным жизненным циклом в простое число лет. Но, как мы вскоре увидим, не только цикады научились использовать синкопированный ритм простых чисел.
Цикады против хищников
Скачайте PDF-файл с веб-сайта «Тайн 4исел». Вырежьте хищников и два семейства цикад. Положите хищников на годы, кратные 6. Каждый игрок берет по семейству цикад. Возьмите три обычные игральные кости с шестью гранями. Сумма чисел, выпавших на трех игральных костях, определит, как часто появляется ваше семейство цикад. Так, если у вас выпало 8, поместите цикаду на каждое число, кратное 8. Но, если на данном месте уже есть хищник, вы не можете разместить там цикаду, например, не можете положить цикаду на 24, потому что это число уже занято хищником. Победителем будет игрок с наибольшим числом цикад на поле. Вы можете модифицировать игру, изменив периодичность, с которой появляется хищник, то есть вместо 6 выбрать другое число.
Во время Второй мировой войны французский композитор Оливье Мессиан был заключенным в концентрационном лагере VIII-A. Среди его сотоварищей были кларнетист, виолончелист и скрипач. Он решил сочинить музыку для квартета – сам он собирался играть на фортепиано. Результатом было одно из величайших музыкальных произведений XX в.: Quatour pour la fin du temps – «Квартет на конец времени». Впервые оно было исполнено для заключенных и надзирателей в концлагере VIII-A. Мессиан играл на расшатанном пианино, которое нашлось в лагере. В первой части, названной «Литургия кристалла», Мессиан хотел создать ощущение нескончаемого времени. Для этого замысла ключевыми оказались простые числа 17 и 29. В то время как скрипка и кларнет обменивались музыкальными темами, представляющими пение птиц, виолончель и фортепиано придавали ритмическую структуру. Партия фортепиано представляет собой ритмическую последовательность из 17 нот, повторяющуюся снова и снова, а накладывающаяся на нее струнная партия содержит период из 29 нот. Поэтому, когда 17-нотный ритм начинается во второй раз, струнная последовательность приближается к двум третям. Результатом выбора простых чисел 17 и 29 является то, что совместная мелодия фортепиано и виолончели начинает повторяться в произведении лишь спустя 17 × 29 нот.
Именно эта постоянно меняющаяся музыка создает ощущение нескончаемости, к которому стремился Мессиан, – и он использует тот же трюк, что и цикады в их противостоянии с хищниками. Представьте, что цикады – это фортепиано, а хищники – виолончель. Различные простые числа 17 и 29 рассинхронизируют эти два инструмента, и произведение заканчивается до того, как музыка начинает повторяться.



Рис. 1.04. «Литургия кристалла» из «Квартета на конец времени» Мессиана. Первая вертикальная линия показывает окончание ритмической последовательности из 17 нот. Вторая линия обозначает конец 29-нотной гармонической последовательности
Мессиан был не единственным композитором, прибегавшим к простым числам в музыке. Использование простого числа было отличительной особенностью Альбана Берга. Как и Дэвид Бекхэм, Берг щеголял числом 23 – можно сказать, был одержим им. Например, в его «Лирической сюите» 23-тактная последовательность определяет структуру произведения в целом. Но также в нем представлен роман, который был у Берга с богатой замужней женщиной. Образ его любовницы создается 10-тактной последовательностью, которая переплетается с характеризующей Берга 23-тактной. Так комбинация математики и музыки воплощает его любовную связь.
Подобно использованию простых чисел Мессианом в «Квартете на конец времени», математика недавно была применена для создания произведения, которое хотя и не является нескончаемым, но повторится лишь спустя тысячу лет. Джем Файнер, один из основателей группы The Pogues, решил создать в лондонском Ист-Энде музыкальную инсталляцию, которая повторится лишь с началом следующего тысячелетия, в 3000 г.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии