Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир Страница 36
Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир читать онлайн бесплатно
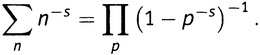
И сумма в левой части, и произведение в правой части простираются до бесконечности. Это, кстати, дает еще одно доказательство того факта, что простые числа никогда не кончаются. Если бы они вдруг кончились, то произведение в правой части содержало бы конечное число множителей, и тем самым мы его немедленно вычислили бы как какое-то число при абсолютно любом аргументе s. [56] При s = 1, однако, левая часть представляет собой гармонический ряд из главы 1, сложение членов которого «уводит нас в бесконечность». Поскольку бесконечность в левой части не может равняться конечному числу в правой, количество простых чисел с необходимостью бесконечно.
V.
Что же такого — как вы, должно быть, недоумеваете — замечательного, такого неординарного и вызывающего имеется в выражении (7.3), что оно удостоилось столь высокопарного имени?
Окончательно это прояснится только в одной из последующих глав, когда мы на самом деле повернем Золотой Ключ. На данный же момент главное, что должно производить впечатление (на математиков оно, во всяком случае, производит большое впечатление), — это что в левой части выражения (7.3) мы имеем бесконечную сумму, пробегающую все положительные целые числа 1, 2, 3, 5, 6, …, а в правой его части — бесконечное произведение, пробегающее все простые числа 2, 3, 5, 7, 11, 13, ….
Выражение (7.3) — Золотой Ключ — на самом деле называется «эйлерова формула произведения». [57] Она впервые увидела свет, хотя и в несколько иной обработке, в статье Variae observationes circa series infinorum, написанной Леонардом Эйлером и опубликованной Санкт-Петербургской академией в 1737 году. (Заглавие переводится как «Различные наблюдения о бесконечных рядах». Прочитайте еще раз оригинальное латинское название и убедитесь в справедливости моего тезиса из главы 4.viii о легкости, с которой читается Эйлерова латынь.) Точная формулировка утверждения о Золотом Ключе в той работе такова.
Theorema 8
Si ex serie numerorum primorum sequens formetur expressio
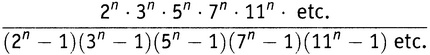
erit eius valor aequalis summae huius seriei
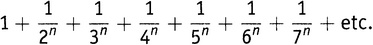
Латынь означает: «Если из последовательности простых чисел образовать следующее выражение…, то его значение будет равно сумме ряда…» Опять же, если вы знакомы с десятком основных латинских окончаний (-orum — родительный падеж; -etur — пассивный залог сослагательного наклонения настоящего времени и т.п.), то эйлерова латынь вас не отпугнет.
Делая наброски идей, из которых выросла данная книга, я сначала полез в математические тексты у себя на книжной полке, чтобы найти доказательство Золотого Ключа, подходящее для читателей, не являющихся специалистами. Я остановился на одном, показавшемся мне подходящим, и включил его в книгу. На более поздней стадии работы над книгой мне подумалось, что стоит, пожалуй, проявить авторское тщание, и я отправился в научную библиотеку (в данном случае — замечательное отделение по наукам, промышленности и бизнесу Нью-Йоркской публичной библиотеки в центре Манхэттена) и отыскал оригинальную статью в собрании трудов Эйлера. Данное им доказательство Золотого Ключа занимает десяток строк и куда проще и изящнее, чем доказательство, которое я извлек из своих учебников. Поэтому я заменил первоначально выбранное доказательство эйлеровым. Доказательство, приведенное в разделе iii этой главы, по сути и есть эйлерово доказательство. Я знаю, что это писательский штамп, но он от этого не перестает быть верным: нет ничего лучше, чем обратиться к первоисточнику.
VI.
После того как мы увидели, что же собой представляет Золотой Ключ, пришло время готовиться к тому, чтобы его повернуть. Для этого понадобится вспомнить некоторое количество математики, включая кусочек дифференциального и интегрального исчислений. В оставшейся части данной главы я приведу все, что нужно знать из дифференциального и интегрального исчисления, чтобы понять Гипотезу Римана и оценить ее значение. А затем, обратив необходимость в удобство, я воспользуюсь этими сведениями, чтобы представить улучшенный вариант ТРПЧ — вариант, имеющий более непосредственное отношение к работе Римана.
Обучение дифференциальному и интегральному исчислению традиционно начинается с графика. График, с которого мы начнем, — тот же, что и изображение логарифмической функции в главе 5.iii; теперь он воспроизведен на рисунке 7.1. Представьте себе, что вы — очень маленький (бесконечно малый, если получится представить) гомункулус, взбирающийся вверх по графику логарифмической функции слева направо. Если вы начали свое путешествие из какой-го точки, находящейся недалеко от нуля, то сначала путь вашего восхождения очень крутой и вам требуется скалолазное снаряжение. Но по мере продвижения ландшафт становится более пологим. К тому времени, как вы достигнете аргументов в районе 10, вы можете распрямиться и просто шагать, как на прогулке.
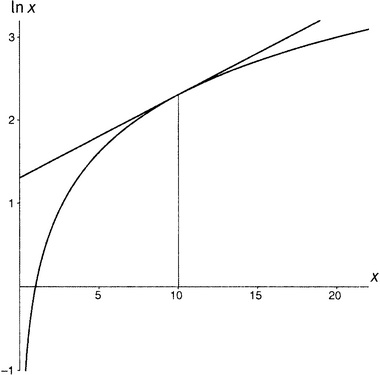
Рисунок 7.1. Функция ln x.
Степень крутизны кривой изменяется от точки к точке. Но в каждой точке наклон кривой имеет определенное численное значение — точно так же, как ваша машина, когда вы разгоняетесь, имеет определенную скорость в каждый данный момент времени — скорость, которую вы фиксируете, бросая взгляд на спидометр. Через мгновение она может слегка измениться, но в каждый определенный момент времени она имеет некоторое определенное значение. Точно так же для любого аргумента в своей области определения (которую составляют все числа, большие нуля) логарифмическая функция имеет некоторый определенный наклон.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии