Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир Страница 35

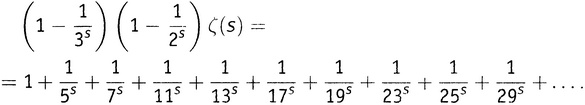
Из бесконечной суммы исчезли все члены, содержащие числа, кратные тройке! Первое выжившее число — это теперь 5.

Умножив теперь обе части полученной формулы на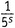, будем иметь

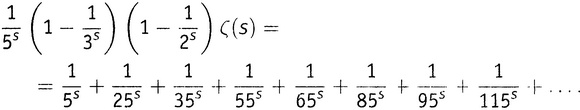
А теперь, вычитая это равенство из предыдущего и рассматривая на этот раз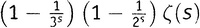 как неделимую конструкцию, видим, что в левую часть одного выражения она входит с множителем 1, а в левую часть другого — с множителем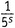. Вычитание дает

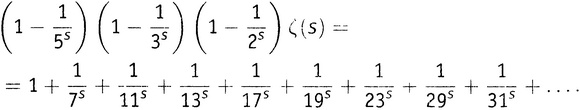
Все слагаемые с числами, кратными 5, исчезли при вычитании, и первое выжившее число в правой части — это 7.

Замечаете сходство с решетом Эратосфена? Но вы должны заметить и отличие. При работе с исходным решетом мы оставляли сами простые числа в неприкосновенности, удаляя только их кратные — числа, полученные из них умножением на 2, 3, 4, …. Здесь же при вычитании мы устраняем из правой части как само простое число, так и все его кратные.

Если продолжать описанную процедуру до достаточно большого простого числа, скажем, до 997, мы получим

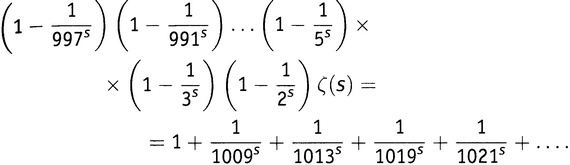
Теперь заметим, что если s — любое число, большее единицы, то правая часть этой формулы совсем ненамного больше чем просто 1. Например, при s = 3 правая часть этой формулы равна 1,00000006731036081534… Поэтому выглядит довольно правдоподобным предположение, что если продолжать указанный процесс до бесконечности, то для любого числа s большего 1 получится следующий результат (7.1):

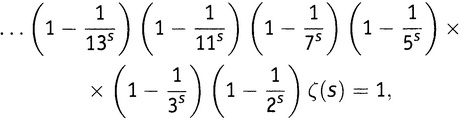
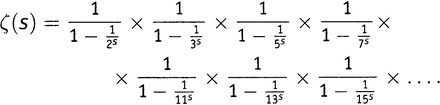
где в левой части содержится ровно одно выражение в скобках для каждого простого числа, причем эти скобки продолжаются налево без конца. Теперь поделим обе части полученного выражения последовательно на каждую из этих скобок (7.2):

IV.

Это — Золотой Ключ. Чтобы он предстал перед нами во всей красе, давайте немного его почистим. Дроби с дробными знаменателями нравятся мне ничуть не больше, чем вам, а кроме того, есть еще полезные математические приемы, которые позволят нам сэкономить на наборе формул.

Прежде всего вспомним 5-е правило действий со степенями: оно говорит, что a^−N есть 1/a^N и a⁻¹ есть 1/a. Поэтому выражение (7.2) можно записать поаккуратнее:

ζ(s) = (1 − 2^−s)⁻¹×(1 − 3^−s)⁻¹×(1 − 5^−s)⁻¹×(1 − 7^−s)⁻¹×(1 − 11^−s)⁻¹×….

Есть даже еще лучший способ. Вспомним про обозначение ∑, введенное в главе 5.viii. Когда мы складываем компанию слагаемых единообразной структуры, их сумму можно записать коротко, используя знак ∑; у этого имеется эквивалент для умножения, когда сомножители имеют единообразную структуру: тогда используется знак ∏. Это заглавная греческая буква «пи», используемая в этом качестве из-за слова «product» (произведение). Используя знак ∏, выражение (7.2) можно переписать таким образом:

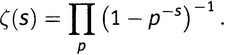
Читается это так: «Дзета от s равна взятому по всем простым числам произведению от величины, обратной единице минус p в степени минус s». Подразумевается, что маленькое p под знаком ∏ означает «по всем простым». ^[55] Вспоминая определение функции ζ(s) в виде бесконечной суммы, можно подставить эту сумму в левую часть и получить

Золотой Ключ (7.3):