Золотой билет. P, NP и границы возможного - Лэнс Фортноу Страница 28

На рисунке ниже вы видите карту Китая, на которой отмечено 71009 городов.

Наложим на карту частую сетку, решим задачу для каждого квадрата в отдельности, а в конце просто соединим все полученные маршруты. Квадраты, в которых оказалось слишком много городов, можно будет раздробить аналогичным образом.

Рис. 6.11. Карта Китая

Этот метод позволяет за разумное время находить коммивояжеру вполне приличные маршруты: длина их отличается от оптимальной всего на несколько процентов.

Если бы все NP-задачи решались приближенными методами настолько замечательно, поднимать вопрос о равенстве или неравенстве P и NP не имело бы особого смысла. Однако в действительности дела обстоят не так уж радужно. Рассмотрим, к примеру, задачу о клике – большой группе людей, в которой все между собой дружны. В общем случае алгоритмы поиска максимальной клики не дают нам хорошего приближения. За разумное время мы вряд ли доберемся даже до клики размера 15; а вдруг в Королевстве есть клика из 2000 жителей?

Если P равно NP, то мы с легкостью отыщем клику любого размера. В противном случае, как выяснилось, нам доступны лишь клики в тысячу раз меньше максимальной. Любой алгоритм, гарантирующий лучшее приближение, позволит находить также и точные решения и докажет равенство P и NP.

Рис. 6.12. Сетка на карте Китая

В большинстве NP-полных задач приближенное решение ищется проще, чем в задаче о клике, но сложнее, чем в задаче коммивояжера. А как обстоит дело с задачей об очень приятных группах?

Мы с вами разобрали тривиальный случай, в котором можно методично перебрать все варианты и убедиться, что минимальная очень приятная группа состоит из четырех человек: Фрэнк, Даниэль, Гарри и Боб. Теперь предположим, что ответ нам неизвестен, и рассмотрим простой приближенный алгоритм поиска очень приятной группы минимального размера.

На первом шаге выберем любых двух друзей и отметим их; пусть это будут Элис и Гарри.

Теперь выберем еще двух друзей, ни один из которых пока не отмечен, и тоже их отметим.

Повторяем до тех пор, пока у нас имеются неотмеченные друзья.

В итоге все те, кого мы отметили, составят очень приятную группу.

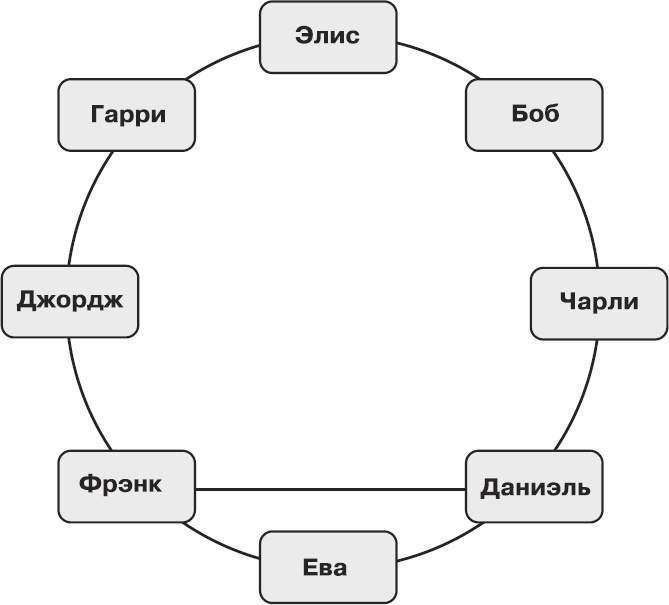
Рис. 6.13. Дружеские связи – II

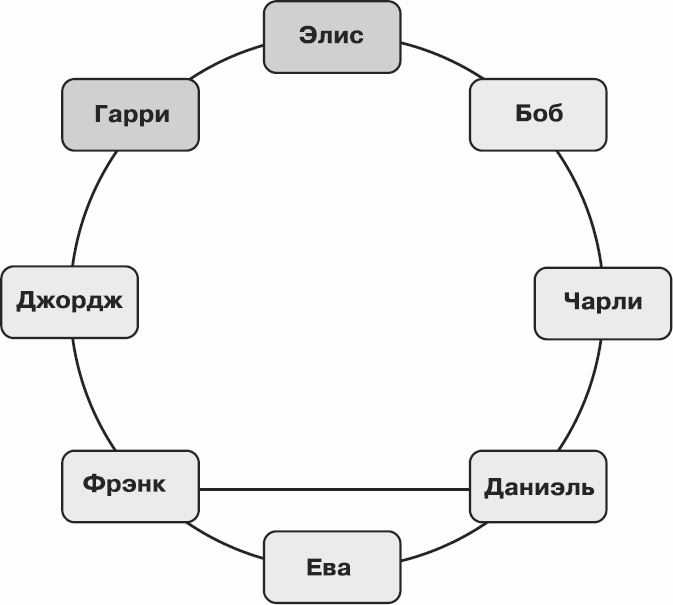
Рис. 6.14. Поиск очень приятной группы – II: шаг 1

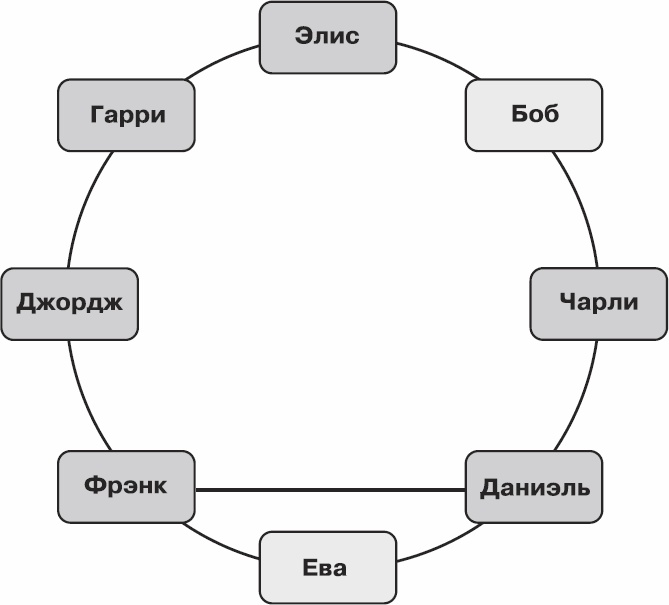
Рис. 6.15. Поиск очень приятной группы – II: шаг 2

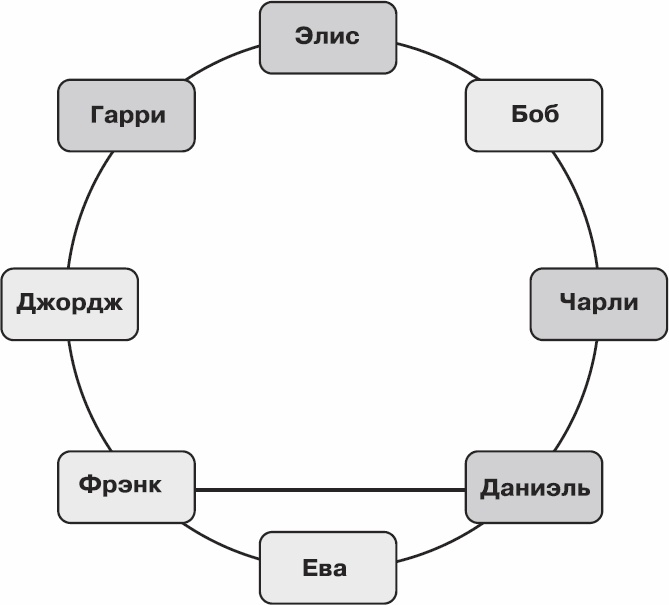
Рис. 6.16. Очень приятная группа размера шесть

В нашем случае получилась очень приятная группа размера шесть. Ясно, что любая очень приятная группа содержит хотя бы одного человека из каждой выбранной дружеской пары, а значит – состоит как минимум из трех человек. Поэтому минимальный размер такой группы лежит в промежутке от трех до шести.

Алгоритм подойдет для любой схемы дружеских связей. Если он, к примеру, отберет 50 дружеских пар и построит очень приятную группу из 100 человек, мы будем знать, что минимальный размер группы – от 50 до 100.

Выходит, мы всегда можем найти очень приятную группу, размер которой превышает минимальный не более чем в два раза. Однако существенно улучшить этот результат нам вряд ли удастся.

Если P равно NP, то мы сможем отыскать минимальную очень приятную группу быстро и эффективно. А если не равно? Тогда в общем случае мы будем получать лишь группы, размер которых превышает минимальный более чем на 36 процентов. Любой алгоритм, гарантирующий превышение ровно в 36 процентов или менее, можно преобразовать таким образом, чтобы он решал произвольную NP-полную задачу. Возможность этого преобразования основывается на целом ряде важных и серьезных результатов, полученных в период между 1990 и 2005 годами.

Рассмотренный выше простейший алгоритм последовательного отбора дружеских пар позволяет получить очень приятную группу, размер которой превышает минимальный не более чем в два раза (т. е. не более чем на 100 процентов). Если P ≠ NP, то мечтать о превышении меньше чем в 36 процентов смысла вообще не имеет. Но, может, удастся создать алгоритм, гарантирующий хотя бы 50-процентное превышение?

В поисках ответа на этот и другие вопросы индийский математик Субхаш Кхот разработал свои «уникальные игры» – модификацию задачи о раскраске карт, в которой для раскраски соседних государств вводятся дополнительные правила. Кхот выдвинул гипотезу, что задача об уникальных играх является NP-полной. Так это или нет – пока никто не знает.

Если гипотеза об уникальных играх верна, то у нас нет шансов придумать хороший приближенный алгоритм: из построений Кхота следует, что в этом случае мы не сможем гарантированно находить очень приятные группы, размер которых превышает минимальный менее чем на 100 процентов. Если гипотеза верна, нам останется довольствоваться описанным выше простейшим алгоритмом.