Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир Страница 27
Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир читать онлайн бесплатно
Гипотеза Римана
Все нетривиальные нули дзета-функции имеют вещественную часть, равную одной второй.
Таблица 5.1 дает нам первое представление о дзета-функции Римана и тем самым представляет собой первый шаг к пониманию Гипотезы Римана.
VII.
Коль скоро в предшествующих разделах данной главы мы потрудились придать смысл степенной функции xa для любого числа a, а не просто для целых чисел, сейчас нет причины ограничивать букву N в выражении (5.1) целыми числами. Можно представить себе, как это число свободно парит, принимая различные значения — дробные, отрицательные и иррациональные. Нет, правда, гарантии, что ряд будет сходиться для всех чисел — как мы уже знаем из главы 1.iii, он не сходится при N = 1. Но можно, по крайней мере, попытать счастья, исследуя разные возможности.
В связи с осознанием этой новой мысли, сменим обозначение N на другую букву, которая имеет меньше традиционных ассоциаций с целыми числами. Очевидным выбором, конечно, была бы буква x. Но Риман в своей работе 1859 года не использовал икса. Подобные вопросы в его время не были урегулированы. Вместо этого он пользовался буквой s; а его работа 1859 года приобрела такое значение, что все математики, жившие после Римана, вслед за ним использовали ту же букву. В исследованиях, посвященных дзета-функции, аргумент всегда обозначается буквой s.
И вот наконец перед нами дзета-функция Римана (дзета, которая пишется как ζ, — это шестая буква греческого алфавита) (5.2):
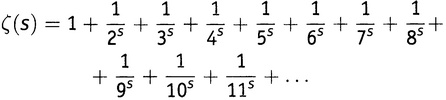
VIII.
Прежде чем двигаться дальше, давайте введем полезные математические обозначения, которые сократят работу по набору формул. (Думаете, легко вставить штуки, подобные выражению (5.2), в Microsoft Word?)
Если математики хотят сложить некоторое множество членов, которые все построены по общему закону, то они используют знак ∑. Это заглавная буква «сигма», восемнадцатая буква греческого алфавита, обозначающая греческую «с» (первую букву в слове «сумма»). Применяется она следующим образом. Суммируемый член, записанный с помощью данного правила, помещается «под» (на самом деле имеется в виду — справа, хотя вопреки логике говорится «под») знаком сигмы. А снизу и сверху от сигмы указывается, где сумма начинается и где заканчивается. Например, выражение
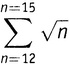
представляет собой математическую «стенографию» — краткую запись выражения √12 + √13 + √14 + √15. Сигма говорит нам: «Сложить их!»; выражения сверху и снизу от сигмы показывают, где начать сложение и где его закончить; и наконец, выражение под знаком сигмы говорит, что, собственно, надо складывать — в данном случае √n.
Математики не особенно педантичны по поводу стиля таких выражений. Приведенную выше сумму часто записывают как
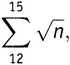
поскольку ясно, что именно n пробегает значения от 12 до 15. Теперь, вовсю используя знак сигмы, мы можем не тратить силы на лишние символы, а записать выражение (5.2) в виде
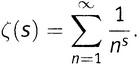
А с учетом 5-го правила действий со степенями это же можно записать как
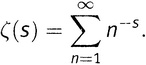
И более того, поскольку n с очевидностью (и часто) используется для обозначения положительных целых чисел 1, 2, 3, 4, …, математики сокращают запись еще сильнее и просто пишут
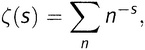
что выражает ту же самую дзета-функцию Римана. Читается это так: «дзета от s определена как взятая по всем n сумма от n в степени минус s». Здесь «по всем n» понимается как «по всем целым положительным п».
IX.
Получив дзета-функцию в виде изящного выражения, посмотрим повнимательнее на ее аргумент s. Из главы 1.iii мы уже знаем, что при s, равном единице, ряд расходится, и, следовательно, у дзета-функции нет значения. При s, равном 2, 3, 4, …, он всегда сходится и тем самым дает значения дзета-функции (см. таблицу 5.1). На самом деле можно показать, что ряд сходится при любом s, большем единицы. При s, равном 1,5, ряд сходится к 2,612375…. При s, равном 1,1, он сходится к 10,584448…. А при s, равном 1,0001, он сходится к 10000,577222…. Может показаться странным, что ряд расходится при s = 1, но при этом умудряется сходиться при s = 1,0001. Это, однако, нормальная ситуация в математике. На самом деле, когда s очень близко к 1, дзета-функция замечательным образом ведет себя подобно функции 1/(s − 1). Эта функция также имеет значения при всех s, кроме того случая, когда s в точности равняется 1, поскольку знаменатель тогда равен нулю, а на нуль делить нельзя.
Некоторую ясность может внести график. На рисунке 5.4 показан график дзета-функции. Как видно, когда аргумент s приближается к 1 справа, значения функции убегают на бесконечность, а когда s само уходит на бесконечность далеко справа, функция все более и более приближается к 1. (Я пририсовал еще два пунктира: линию s = 1 и график постоянной функции.)
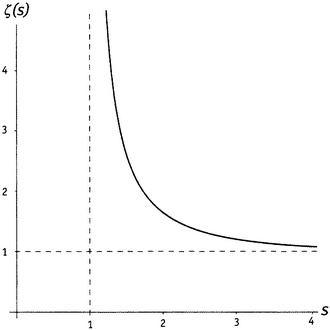
Рисунок 5.4. Дзета-функция для аргументов, превышающих 1.
На графике не показано ничего про дзета-функцию слева от линии s = 1. Это потому, что до сих пор мы предполагали, что s больше единицы. А если меньше? Если, скажем, s равно нулю? Ну, тогда выражение (5.2) примет вид
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии