Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир Страница 26
Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир читать онлайн бесплатно
Такое нелегко себе представить. Функции (ln x)N растут быстро — и даже очень быстро. И тем не менее, если на рисунке 5.3 отойти достаточно далеко на восток, то рано или поздно, при некотором впечатляюще большом аргументе, каждая из них опустится ниже кривой x0,3, x0,2, x0,1 и вообще любой кривой из этого семейства, какую вы только потрудитесь нарисовать. Придется отправиться на восток в окрестность точки x = 7,9414×103959, прежде чем (ln x)100 опустится ниже, чем x0,3; и однако же это случится.
V.
Кое-что из сказанного понадобится нам прямо сейчас, а кое-что останется на потом. Но все сказанное важно для понимания Гипотезы Римана, и я призываю вас проконтролировать некоторые основные моменты — проверить, как вы их понимаете, прежде чем двигаться дальше. Для этого сгодится карманный калькулятор. Можете, например, найти ln 2 (он равен 0,693147…) и ln 3 (равный 1,098612…) и удостовериться, что при сложении их действительно получается ln 6 (равный 1,791759…). Но только обратите, пожалуйста, внимание, что (как я уже упоминал) прежде использовались логарифмы по основанию 10, так что клавиша «log» на многих карманных калькуляторах вычисляет именно десятичные логарифмы. Тот единственный логарифм, который нас здесь интересует, — логарифм по основанию e — на калькуляторе, как правило, вычисляется с помощью альтернативной клавиши, помеченной ln x. Вот эта клавиша вам и нужна. (Буква n указывает на «натуральный» логарифм; логарифм по основанию e по всем правилам называется «натуральный логарифм».)
Ну а теперь вернемся к базельской задаче.
VI.
Эйлерово решение базельской задачи прекрасно иллюстрирует сделанное в разделе I этой главы замечание, что поиск решений в замкнутом виде расширяет понимание, позволяя проникнуть в суть вещей. Эйлерово решение дало не только замкнутое выражение для ряда из обратных квадратов, но в качестве побочного продукта еще и замкнутые выражения для рядов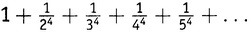 ,
,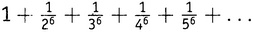 и т.д. Для четных N результат Эйлера дает в замкнутом виде точное значение для следующего бесконечного ряда (5.1):
и т.д. Для четных N результат Эйлера дает в замкнутом виде точное значение для следующего бесконечного ряда (5.1):
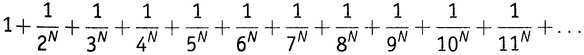
Когда N равно двум, ряд сходится к π2/6, как уже было сказано; когда N равно 4, ряд сходится к π4/90; когда N равно 6, ряд сходится к π6/945 и т.д. Метод Эйлера дает ответ для каждого четного N. В более поздней публикации он сам добрался до N = 26, когда ряд сходится к числу 1 315 862π26/11 094 481 976 030 578 125.
А что, если N нечетное? Полученный Эйлером результат ничего про это не говорит. Как не говорит и ни один другой результат, полученный за последующие 260 лет. Нет никаких идей относительно замкнутого выражения (если таковое вообще существует) ни для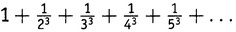 , ни для аналогичного ряда при других нечетных показателях степени. Никто не смог найти замкнутое выражение для этих рядов. Мы знаем, что они сходятся, и можем, конечно, методом грубой силы вычислить их значение с любой требуемой точностью. Мы просто не знаем, что они означают. Только в 1978 году было доказано, что ряд
, ни для аналогичного ряда при других нечетных показателях степени. Никто не смог найти замкнутое выражение для этих рядов. Мы знаем, что они сходятся, и можем, конечно, методом грубой силы вычислить их значение с любой требуемой точностью. Мы просто не знаем, что они означают. Только в 1978 году было доказано, что ряд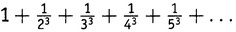 определяет иррациональное число. [40]
определяет иррациональное число. [40]
Итак, к середине XVIII века немало математиков задумывались над бесконечным рядом из выражения (5.1). Точные значения — замкнутый вид — были известны для всех четных чисел N, тогда как для нечетных можно было получать приближенные значения, беря сумму достаточного числа членов. Не будем забывать, что, когда N равно 1, соответствующий ряд становится просто гармоническим рядом, который расходится. В таблице 5.1 приведены значения выражения (5.1) (которое, напомним, есть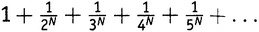 ) с точностью до 12 знаков после запятой.
) с точностью до 12 знаков после запятой.
| N | Значение выражения (5.1) | |
|---|---|---|
| 1 | (нет значения) | |
| 2 | 1,644934066848 | |
| 3 | 1,202056903159 | |
| 4 | 1,082323233711 | |
| 5 | 1,036927755143 | |
| 6 | 1,017343061984 | |
Таблица 5.1.
Эта таблица похожа на один из тех «мгновенных снимков» некоторой функции, которые мы рассматривали в главе 3.iv. Так примерно дело и обстоит. Вспомним утверждение Гипотезы Римана, приведенное во вступлении.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии