Истина и красота. Всемирная история симметрии - Йен Стюарт Страница 24
Истина и красота. Всемирная история симметрии - Йен Стюарт читать онлайн бесплатно
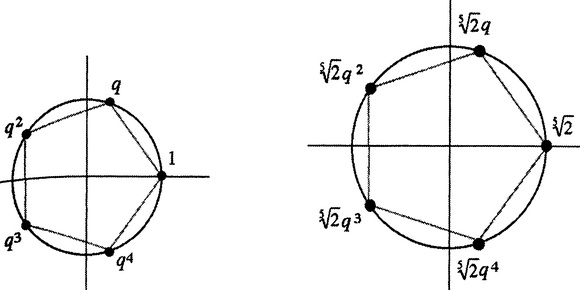
Слева: корни пятой степени из единицы в комплексной плоскости.
Справа: корни пятой степени из двух.
Все это очень мило, но здесь же содержится намек на нечто гораздо более глубокое. Корни пятой степени из 2 можно рассматривать как решения уравнения x5 = 2. Это уравнение пятой степени, и у него пять комплексных решений, причем только одно из них вещественно. Аналогичным образом уравнение x4 = 2 имеет четыре решения (все корни четвертой степени из 2), уравнение на корни 17-й степени из 2 имеет 17 решений и так далее. Не обязательно быть гением, чтобы подметить правило: число решений равно степени уравнения.
То же самое, как представлялось, выполняется не только для уравнений на корни п-й степени, но и вообще для любого алгебраического уравнения. Математики пребывали в убеждении, что в области комплексных чисел каждое уравнение имеет ровно столько решений, какова степень уравнения. (Технически это утверждение верно, только когда решения подсчитываются с учетом их «кратностей». Если это соглашение не использовать, то число решений равно степени уравнения или меньше ее.) Эйлер доказал это свойство для уравнений степеней 2, 3 и 4 и утверждал, что аналогичные методы будут работать и в общем случае. Его идеи выглядели правдоподобно, но заполнение пробелов в намеченной им схеме доказательства оказалось практически невозможным, и даже сегодня требуются серьезные усилия, чтобы довести метод Эйлера до логического конца. Тем не менее математики предполагали, что если они решают уравнение некоторой степени, то следует ожидать появления в точности стольких корней, какова эта степень.
По мере того как Гаусс развивал свои идеи в теории чисел и анализе, его все менее и менее удовлетворяло то, что никто не доказал это предположение. Характерно, что в конце концов он сам предложил доказательство. Оно было сложным и на удивление непрямым: любой квалифицированный математик мог убедиться в его верности, но никто не мог сообразить, как же Гаусс до него додумался. Математический лис мстительно вилял хвостом.
В переводе с латыни заглавие диссертации Гаусса звучало как «Новое доказательство, что каждую рациональную целую функцию одного переменного можно разложить на вещественные множители первой или второй степени». Если пробиться через профессиональные термины, принятые в то время, то заглавие утверждает, что каждый многочлен (с вещественными коэффициентами) равен произведению выражений, представляющих собой линейные или квадратичные многочлены.
Гаусс использовал слово «вещественные», чтобы ясно показать: он работает в рамках традиционной числовой системы, в которой отрицательные величины не имеют квадратных корней. В наши дни мы бы выразили теорему Гаусса в логически равносильном, но более простом виде: каждый вещественный многочлен степени n имеет n вещественных или комплексных корней. Но Гаусс тщательно подбирал выражения таким образом, чтобы его работа не опиралась на все еще несколько сбивающую с толку систему комплексных чисел. Комплексные корни вещественного многочлена всегда можно собрать в пары, что приводит к вещественным квадратичным множителям, а линейные множители отвечают вещественным корням. Сформулировав заглавие в терминах множителей этих двух типов («множители первой или второй степени»), Гаусс обошел стороной спорный вопрос о комплексных числах.
Одно слово в заглавии не оправданно: «новое» предполагает, что имеются «старые» доказательства. Гаусс дал первое строгое доказательство этой фундаментальной теоремы в алгебре. Но чтобы не обижать прославленных предшественников, утверждавших, что у них имелись доказательства — которые все оказались ошибочными, — Гаусс представил свое выдающееся достижение как всего лишь самое свежее доказательство, опирающееся на новые (то есть правильные) методы.
Эта теорема получила известность как Основная Теорема Алгебры. Гаусс считал ее настолько важной, что дал в общей сложности четыре доказательства, причем последнее — когда ему было 70 лет. Лично он не испытывал никаких колебаний или сомнений по поводу комплексных чисел: они играли значительную роль в его мыслительном процессе, и впоследствии он сформировал собственное объяснение их смысла. Однако он старался избегать разногласий. С годами он стал замалчивать многие из своих оригинальных идей — неэвклидову геометрию, комплексный анализ и строгий подход к комплексным числам, — потому что не хотел вызывать то, что он называл «плачем беотийцев».
Гаусс не ограничивался чистой математикой. В начале 1801 года итальянский священник и астроном Джузеппе Пьяцци открыл новую планету или то, что ему представлялось планетой, — тусклое пятно света в телескопе, от ночи к ночи менявшее свое положение на фоне звезд, что было верным признаком принадлежности тела к Солнечной системе. Планете должным образом дали имя Церера [21], но на самом деле это оказался астероид — первый открытый астероид в истории. Не успел Пьяцци обнаружить новый мир, как тут же потерял его в блеске Солнца. Он сумел сделать так мало наблюдений, что астрономы не могли вычислить орбиту нового тела и беспокоились, что не найдут его, когда оно снова выйдет из-за Солнца.
Это была задача, достойная Гаусса, и он охотно за нее взялся. Он изобрел улучшенные способы определения орбит исходя из малого числа наблюдений и предсказал, где должна появиться Церера. Когда так и произошло, молва о Гауссе распространилась повсеместно. Путешественник и естествоиспытатель Александр фон Гумбольдт попросил Пьера-Симона де Лапласа — специалиста по небесной механике — назвать величайшего математика в Германии и получил ответ: «Пфафф». Когда недоумевающий Гумбольдт спросил: «А Гаусс?» — Лаплас ответил: «Гаусс — величайший математик в мире».
К сожалению, новоявленное светило отвлекло его от чистой математики на длинные вычисления для расчета орбиты, что можно было считать растратой его неординарных способностей. Не в том дело, что небесная механика не важна, — просто эту работу могли бы проделать и другие, менее талантливые математики. С другой стороны, из-за этого его дальнейшая жизнь полностью устроилась. Гаусс уже некоторое время искал постоянное место работы, которое оставляло бы возможность для общественного служения, с тем чтобы отдать должное своему покровителю — герцогу. Его работа о Церере привела к тому, что он стал директором Геттингенской обсерватории, и этот пост он занимал всю свою научную жизнь.
В 1805 году он женился на Иоанне Остхофф. В письме к Бойяи он так описывал свою новую жену: «Прекрасное лицо Мадонны, зерцало мира и здоровья, нежные, несколько мечтательные глаза, безупречная фигура — это одна сторона; яркий ум и развитая речь — это другая; но мягкая, безмятежная и целомудренная душа ангела, не причиняющая зла ни одному созданию, — это лучшее». Иоанна родила ему двоих детей, но в 1809 году умерла при родах, и убитый горем Гаусс «закрыл ее ангельские глаза, в которых я видел свой рай последние пять лет». Он начал страдать от одиночества, впал в депрессию, и жизнь уже никогда не была для него прежней. Он нашел новую жену — лучшую подругу Иоанны Минну Вальдек, но брак был не самым счастливым, несмотря на рождение еще троих детей. Гаусс постоянно спорил с сыновьями, а дочерям указывал, что им следует делать, и молодым людям настолько надоело это терпеть, что они уехали из Европы в Соединенные Штаты, где в дальнейшем преуспели.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии