Прокачай мозг методом Павла Дурова - Светлана Кузина Страница 4
Прокачай мозг методом Павла Дурова - Светлана Кузина читать онлайн бесплатно
Ознакомительный фрагмент

Проведите три прямые линии таким образом, чтобы отделить собачек от косточек.
3. Поиграем в домино
При помощи четырех костей домино можно изобразить умножение трехзначного числа на однозначное. На рисунке показан пример 551×4=2204. И 28 костей домино можно сложить 7 «умножений», подобных показанному на рисунке. Шесть «умножений» вы построите без особого труда. А вот над седьмым придется подумать – все же это возможно.

4. Пересадим деревья
У Джона был небольшой парк из десяти деревьев, которые располагались в два ряда по пять деревьев. Ему показалась такая рассадка очень скучной и Джон решил пересадить эти деревья таким образом, чтобы после пересадки они образовали между собой пять рядов, по четыре дерева в каждом ряду.
Как ему это удалось?

5. Поймаем бабочек
Разместите восемь бабочек на линиях рисунка так, чтобы на каждой окружности и на каждой из четырех прямых линий было по две бабочки.
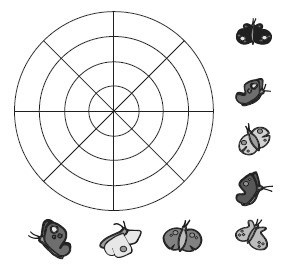
6. Поможем Алисе
Эту задачу придумал английский математик Чарлз Доджсон, он же Льюис Кэрролл, автор известной детской книги “Алиса в стране чудес”.
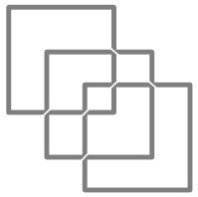
Вам необходимо нарисовать фигуру, указанную на рисунке не отрывая карандаша от бумаги и не проводя дважды одну и ту же линию. Задача усложняется тем, что линии не должны нигде пересекаться между собой (допускается только угловое касание линий).
7. Узнаем название книги
В этом ребусе зашифровано название книги братьев – фантастов.

8. Нарисуем орнамент
Оригинальный орнамент, изображенный на рисунке, состоит из 16 маленьких треугольников. Некоторые группы из четырех соседних маленьких треугольников образуют большие треугольники. В орнаменте прорисовано шесть больших треугольников, «сплетенных» между собой.
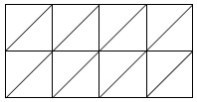
Вам необходимо вписать в каждый маленький треугольник орнамента одно из целых чисел от 1 до 16 (не повторяя их) таким образом, чтобы сумма чисел в любом из шести больших треугольников равнялась 34.
9. Сосчитаем треугольники
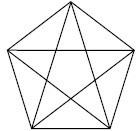
Данная геометрическая фигура включает в себя множество треугольников.
Проверьте свою геометрическую смекалку и сосчитайте сколько их.
10. Расставим флажки
На главной площади провинциального городка шла подготовка к празднику 9 Мая. Ученикам местной школы было поручено украсить площадь гирляндами, шарами и флагами. Флагов было лишь 12. Сначала школьники расставили их по 4 штуки с каждой стороны как показано на рисунке.
Потом сообразили, что эти же 12 флагов они могут расставить по 5 и даже по 6 с каждой стороны.
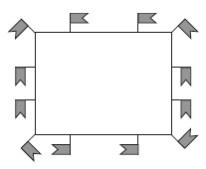
Покажите на схеме, как ученики расставили 12 флагов по 5 с каждой из четырех сторон и как они могли бы их расставить по 6.
11. Погоняем шары
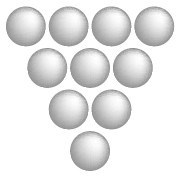
Переложите всего три шарика, так чтобы получился точно такой же треугольник, но перевернутый вверх ногами.
12. Выберем нужные слова
В столбике слева 14 слов. В каждом слове, начиная со второго, число букв на одну больше, чем в предыдущем. В последнем слове «самообразование» – 15 букв.
Из всех этих четырнадцати слов выберите четыре слова так, чтобы были справедливыми следующие два равенства:
a2=bd, ad=b2c
Через а, b, c и d здесь обозначены количества букв соответственно в первом, втором, третьем и четвертом словах, выбранных вами.
УМ
МИР
ФЛАГ
ПОБЕДА
СВОБОДА
ЕДИНСТВО
СОЦИАЛИЗМ
МАТЕМАТИКА
РАЗМЫШЛЕНИЕ
КВАЛИФИКАЦИЯ
ВООДУШЕВЛЕНИЕ
ЭЛЕКТРИФИКАЦИЯ
САМООБРАЗОВАНИЕ
Какие это слова?
13. Зажгем звездочки
В одной из белых клеток расположена 1 звездочка. Вам необходимо разместить в белых клетках еще 7 звездочек таким образом, чтобы никакие 2 звездочки (из восьми) не находились на одной горизонтали или вертикали, или какой-либо диагонали.
Решать задачу придется методом проб, поэтому дополнительный интерес задачи состоит том, чтобы в процесс необходимых испытаний внести известную систему.
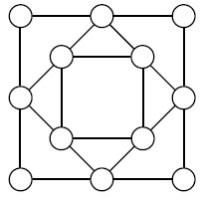
14. Поиграем в кристалл
На рисунке изображена часть химической кристаллической решетки. Атомы данной решетки соединены линиями между собой в десять рядов по три атома в каждом. Необходимо подобрать 13 целых чисел, из них 11 различных и 2 одинаковых и вписать их в атомы. В итоге, сумма чисел в каждом ряду вдоль линий должна равняться 20. Наименьшее из искомых чисел равно 1, а наибольшее равно 15.
15. Заглянем в окошки
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии