Планк. Квантовая теория - Alberto Tomas Perez Izquierdo Страница 14

S = k ln Ω.

Для расчета Ω необходимо знать, сколько возможных конфигураций имеет система при общей энергии всех осцилляторов. Для того чтобы узнать количество конфигураций, Планк воспользовался предположением, что энергия разделяется на дискретные элементы величиной ε. Чтобы исполнялся закон смещения Вина, Планк был вынужден уточнить, что эти элементы энергии, как он их назвал, должны быть пропорциональны частоте п согласно формуле:

ε = hv.

Эти дискретные элементы позже получили название квантов, а представленное выше выражение было названо квантовой гипотезой. Обозначение h — константа, равная 6,62606957(29) · 10^~34Дж/Гц, сейчас называется постоянной Планка.

Второе начало термодинамики позволяет использовать энтропию для расчета соотношения между энергией и температурой. После ряда преобразований Планк получил:

u_v = 8πh/c³ ∙ v³/h^v/kT.

Это та же формула, которую Планк предложил в октябре, но ее новый вид позволяет получить точные выражения для двух констант, С и а, появляющихся в законе. Их величина — С = 8πh/c³ и а = h/k — связывает эти две константы с другими постоянными, такими как скорость света с и постоянная Больцмана k. Весьма важно появление последней константы, взятой из определения энтропии. В последней главе мы рассмотрим некоторые важнейшие следствия отношений между разными постоянными.

Еще раз рассмотрим концептуальные элементы доказательства Планка.

— Электродинамика позволяет сформулировать отношение между механической энергией осциллятора и электромагнитным полем, с которым энергия находится в равновесии. Это отношение строится на предположении, что осциллятор поглощает столько же энергии, сколько излучает. Как можно было ожидать, отношение не зависит от физических характеристик осциллятора, таких как заряд или масса, но связано с частотой и универсальной константой — скоростью света. Это соответствует закону Кирхгофа, согласно которому спектральное распределение излучения не может зависеть от физических характеристик вещества, из которого изготовлены стенки полости.

— Второе начало термодинамики позволяет получить соотношение между внутренней энергией и температурой из выражения энтропии.

— Наконец, вероятностная интерпретация энтропии Больцмана позволяет рассчитать энтропию системы осцилляторов.

Математический вывод закона Планка

Для расчета энтропии взаимодействующих осцилляторов определенной частоты S = klnΩ необходимо рассчитать количество возможных конфигураций Ω. Это количество зависит от всех доступных способов распределения элементов энергии Р величиной ε между количеством осцилляторов, равным Ν. Обозначим элементы энергии кружками, границы элементов, соответствующих одному осциллятору, — крестиками. Любую конфигурацию можно записать в следующем виде.

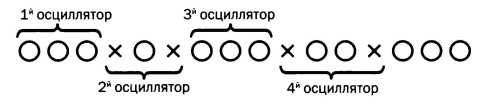
Этот пример означает, что у первого осциллятора имеется три элемента энергии, у второго — один, у третьего — три, у четвертого — два и так далее. Возможное количество конфигураций нам дает комбинаторика, согласно которой:

Ω = (N + Р-1)!/Р!(N-1)!.

В цепочке у нас есть N + Р - 1 символов. Факториал в числителе означает все возможные комбинации крестиков и кружков. Факториалы в знаменателе показывают, что порядок, в котором идут кружки и крестики, не имеет значения, так как осцилляторы и элементы энергии неразличимы. Планк прибегнул к известному приближению, формуле Стирлинга, по которой Inn! = nlnn - n. И так как N и Р значительно больше единицы, получается:

S = k[(N + Р)lп(N + Р) - PlnP - N/ln/N].

Пользуясь тем, что UN = Pε, и вводя среднюю энергию каждого осциллятора, U_N= NU, Планк пришел к следующему выражению:

S = к[(1 + U/ε)ln(1 + U/ε) - (U/ε)lnU/ε].

Для того чтобы выражение энергии, получаемое из выражения выше, соответствовало закону смещения Вина, Планк доказал, что S может быть только функцией частного U/v. Это заставляет прибегнуть к гипотезе ε = hv, в которой h — константа, называемая сегодня постоянной Планка. С учетом этого получается:

S = к[(1 + U/hv)ln(1 + U/hv) - (U/hv)lnU/hv].

Второе начало термодинамики дает нам отношение между энергией и температурой:

1/T = dS/dU

Вычисляя производную и U, мы получаем среднюю энергию осциллятора:

U_v = hv/(e^hv/kT - 1)

Используя отношение между энергией осциллятора и электромагнитным полем, с которым он находится в равновесии, получаем выражение:

u_v = 8πh/c³·v³/(e^hv/kT - 1)

которое представляет спектральное распределение энергии, обнаруженное Планком эмпирическим путем.

К этим факторам Планк добавил квантовую гипотезу, необходимую для выполнения закона, правильность которого была доказана эмпирически. Также отметим, что каждый осциллятор может поглощать и испускать энергию излучения в величине, пропорциональной V. Когда осциллятор поглощает или испускает электромагнитное излучение, его энергия

увеличивается или уменьшается на величину hν. Кроме того, энергия осцилляторов квантуется. Энергия осциллятора с частотой v может принимать следующие величины: hv, 2hv, 3hv, ..., nhv.

Из всех этих составляющих, на взгляд Планка, самой значимой была не квантовая теория, а необходимость прибегнуть к вероятностной интерпретации Больцмана. Нужно понимать, что в конце века электродинамика и термодинамика были достаточно изучены, при этом идеи Больцмана вызывали довольно бурную полемику, особенно в Германии. И Планк стал первым из физиков после самого Больцмана, который использовал его методы. Тот факт, что идеи Больцмана привели его к успеху, поразил самого Планка, и по сравнению с этим квантовая гипотеза отходила на второй план. Как мы увидели, Планк был вынужден прибегнуть к ней, чтобы достичь нужного результата, а именно соответствия закону, который он открыл несколькими месяцами ранее и скрупулезно вместе с Рубенсом проверил его соответствие экспериментальным данным. Только использование квантовой теории позволяло привести расчет вероятностных состояний системы осцилляторов к ожидаемому результату.

Если статьи Эйнштейна (1879-1955) или Шрёдингера (1887-1961) можно сравнить с сочинениями Моцарта, они наполнены вдохновением и внутренней логикой, то статья Планка, опубликованная в 1901 году в Annalen der Physik, похожа на джазовую композицию, а его формула ε = hν — на гениальную импровизацию.