Алгоритмы для жизни. Простые способы принимать верные решения - Том Гриффитс Страница 13

В популярной телеигре «Сделка?!» участник выбирает один из 26 портфелей, в которых находятся призы от одного цента до миллиона долларов. По ходу игры таинственный персонаж по имени Банкир периодически звонит и предлагает участнику различные суммы, чтобы тот не открывал выбранный портфель. Задача участника – решить, какую названную Банкиром сумму предпочесть неизвестному призу в чемодане.

Гиттинс (пусть и за много лет до выхода в эфир первого выпуска игры) понял, что проблема многорукого бандита ничем не отличается. О каждом игровом автомате мы знаем крайне мало, а то и вовсе ничего, но есть некая гарантированная сумма выигрыша, которая, если нам предложат ее взамен игры на автомате, заставит нас больше никогда не дергать этот рычаг. Эта цифра, которую Гиттинс назвал «динамический индекс распределения» и которую весь мир знает сегодня как индекс Гиттинса, предлагает очевидную стратегию поведения в казино: всегда играйте на автомате с наивысшим индексом ^[6].

По факту стратегия индексирования оказалась удачной. Она полностью решает проблему многорукого бандита с геометрически дисконтированными выигрышами. Напряженные взаимоотношения между исследованием и эксплуатацией превращаются в более простую задачу по максимизации единственной величины, которая составляет долю и того и другого. Гиттинс скромно оценивает свои достижения: «Это, конечно, не великая теорема Ферма, – говорит он со смешком, – но это теорема, позволяющая решить ряд вопросов дилеммы "исследование/эксплуатация"».

Расчет индекса Гиттинса для конкретного агрегата, учитывая показатели его работы и нашу ставку дисконтирования, используется и сегодня. Но как только индекс Гиттинса для определенного набора предпосылок становится известен, он может в дальнейшем использоваться для решения всех задач такого плана. Примечательно, что количество рычагов не имеет значения, поскольку индекс для каждого рассчитывается отдельно.

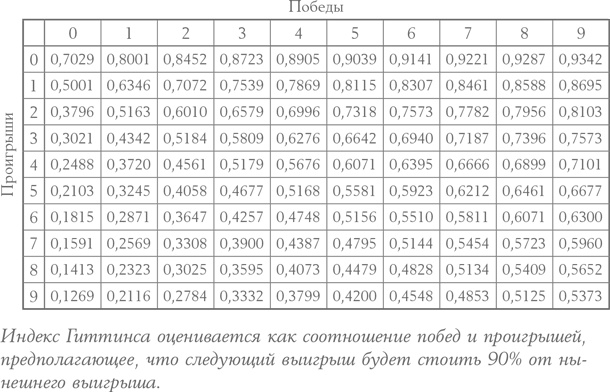
В таблице ниже приведены значения индекса Гиттинса для девяти успехов и неудач с тем расчетом, что выигрыш в следующей игре будет стоить 90 % от выигрыша нынешнего. Эти значения могут использоваться для решения задач многорукого бандита в повседневных делах. Например, руководствуясь данными предположениями, вы должны выбрать тот игровой автомат, у которого результат прошлых игр 1: 1 (и ожидаемая ценность 50 %), а не тот, у которого результат 9: 6 (и ожидаемая ценность 60 %). Сравнение соответствующих значений в таблице показывает, что у менее известного автомата индекс 0,6346, а у другого индекс всего 0,6300. Проблема решена: испытай удачу в этот раз и исследуй.

Глядя на таблицу значений индекса Гиттинса, можно отметить несколько интересных моментов. Во-первых, наглядно показано, как работает принцип «оставайся победителем»: в любой строке слева направо значение индекса возрастает. То есть если вы выбрали автомат, дернули за рычаг и получили выигрыш, то (согласно таблице) имеет смысл снова дергать именно его. Во-вторых, можно увидеть, в каких случаях принцип «проиграл – переключись» может вас подвести. Девять выигрышей подряд и следующий за ними проигрыш дадут индекс 0,8695, который выше других значений в таблице, и, таким образом, вам нужно оставаться у этого автомата по меньшей мере еще на одну игру.

Но самое интересное в таблице можно увидеть в верхнем левом углу. Результат 0: 0 – у автомата, который совершенно неизвестен, – обладает ожидаемой ценностью в 0,5000, а индекс Гиттинса – 0,7029. Иными словами, нечто неизведанное не является более привлекательным, чем автомат, который, как вы уже знаете, выдает деньги в семи играх из десяти! Если посмотреть по диагонали вниз, можно заметить, что соотношение 1: 1 дает в итоге индекс 0,6346, соотношение 2: 2 дает индекс 0,6010 и т. д. Если тенденция к 50 %-ным выигрышам сохраняется, то мы в итоге приходим к индексу 0,5000, тогда как практика доказывает, что в автомате нет ровным счетом ничего особенного и он в итоге забирает тот «бонус», который подталкивает нас к дальнейшему исследованию. Но конвергенция происходит довольно медленно; азарт исследователя – это все же мощная сила. И действительно, смотрите: даже неудача с самой первой игры (соотношение 0: 1) имеет индекс по-прежнему выше 50 %.

Мы также можем заметить, насколько меняется баланс «исследовать/эксплуатировать» по мере того, как мы «обесцениваем» будущее. В следующей таблице представлена точно такая же информация, как в предыдущей, но предполагается, что последующий выигрыш стоит 99 % от нынешнего, а не 90 %. В будущем, продуманном столь же четко, как настоящее, ценность случайного открытия, относящегося к принятию беспроигрышных решений, возрастает еще больше. Здесь игра на абсолютно непроверенном автомате с результатом 0: 0 имеет 86,99 % гарантированного успеха!

Индекс Гиттинса, таким образом, дает нам формальное строгое обоснование, почему мы всегда предпочитаем узнавать нечто новое при условии, что у нас есть некоторая возможность воспользоваться результатами исследования. Старая пословица утверждает, что «по ту сторону забора трава всегда зеленее», а математика объясняет, почему это так: у неизведанного всегда есть шанс оказаться лучше, даже если мы не ожидаем особой разницы и даже если оно может оказаться хуже. Непроверенный новичок ценится больше (на ранних этапах, во всяком случае), чем ветеран с такими же, казалось бы, способностями именно потому, что о новичке мы меньше знаем. Исследование ценно само по себе, поскольку поиски нового увеличивают наши шансы найти лучшее. Таким образом, именно расчет на будущее, а не концентрация на сегодняшнем дне и побуждает нас к новшествам.

Из этого следует, что индекс Гиттинса предлагает удивительно простое решение проблемы многорукого бандита. Но это вовсе не обязательно ставит точку в данном вопросе или помогает нам ориентироваться во всех соотношениях исследования/эксплуатации в повседневной жизни. С одной стороны, индекс Гиттинса оптимален только при определенных строгих условиях. Он основан на обесценивании будущих выигрышей в геометрической прогрессии, оценивая каждый на долю меньше предыдущего, то есть делая ровно то, чего, согласно многочисленным исследованиям в области бихевиористской экономики и психологии, люди обычно не делают. Но если появляются затраты на переключение между разными вариантами, индекс Гиттинса перестает быть оптимальным. (Трава по ту сторону забора, может быть, и зеленее, но это не обязательно служит основанием для того, чтобы лезть через забор – не говоря уж о том, чтобы взять второй ипотечный кредит.) И, вероятно, еще более важно то, что индекс Гиттинса невозможно вычислить походя, на лету. Если вы постоянно таскаете с собой таблицу значений индекса, то вы, конечно, можете оптимизировать свой выбор кафе и ресторанов, но затраченные время и усилия могут не стоить того. («Погодите, сейчас я разрешу наш спор. Так, этот ресторан получил 29 хороших оценок из 35, а этот – 13 из 15, и, таким образом, индекс Гиттинса… Эй, а куда все ушли?!»)