Площадь и башня. Cети и власть от масонов до Facebook - Ниал Фергюсон Страница 11

Формальное изучение сетей началось в середине XVIII века, когда переживал пору расцвета восточнопрусский город Кёнигсберг, родина философа Иммануила Канта. Среди достопримечательностей Кёнигсберга были семь мостов через реку Прегель ^[124], соединявших противоположные берега с двумя островками посреди реки, а также сами эти островки между собой (см. илл. 4). Местные жители давно заметили, что невозможно пройти по всем семи мостам, не пройдя по одному из них хотя бы дважды ^[125]. Эта задача привлекла внимание великого математика Леонарда Эйлера, уроженца Швейцарии, и в 1735 году он разработал теорию графов, чтобы наглядным и научным способом доказать, почему такой маршрут невозможен. На упрощенном графе, или схеме (см. илл. 5), четыре “вершины” обозначают два берега реки и два острова, больший и меньший, а семь “ребер” обозначают соединяющие их мосты. Строго говоря, Эйлер продемонстрировал, что возможность существования пути, который пересекал бы каждое ребро всего один раз, зависит от степени вершин (то есть количества ребер, сходящихся к каждой вершине). Граф должен иметь либо две вершины с нечетным количеством ребер, либо ни одной. Поскольку в графе, изображающем семь кёнигсбергских мостов, четыре таких вершины (одна с пятью ребрами, остальные с тремя), Эйлеров путь в нем невозможен. Пройтись по всем мостам, не пройдя ни по одному из них дважды, можно было бы, только убрав одно ребро – то есть мост между двумя островами: тогда остались бы только две вершины с нечетной степенью. Со времен Эйлера основными единицами теории графов, которую он сам изначально называл “геометрией положения”, являются вершины (узлы) и ребра (звенья).

В XIX веке ученые стали применять этот принцип ко всему – от картографии до электрических цепей и до изомерии органических соединений ^[126]. О том, что могут существовать еще и общественные сети, тоже, разумеется, задумывались крупные политические мыслители того времени – в частности, Джон Стюарт Милль, Огюст Конт и Алексис де Токвиль. Последний из них обратил внимание на то, что большое количество разного рода общественных объединений на раннем этапе существования США сыграло важную роль в формировании американской демократии. Однако ни один из них не пытался изложить свои догадки в связной форме. Поэтому можно считать, что изучение социальных сетей ведет свой отсчет с 1900 года, когда школьный учитель и обществовед-любитель Иоганн Делитч опубликовал схему, отображавшую характер дружеских отношений между 53 учениками, с которыми он занимался в течение 1880/81 учебного года ^[127]. Делитч выявил четкую связь между близостью общественного положения мальчиков и их академической успеваемостью (на основе которой в ту пору рассаживали учеников в классе). В чем-то сходная работа была проделана тремя десятилетиями позже в Нью-Йорке, где психиатр Якоб Леви Морено, своеобразная личность – австриец по рождению ^[128], но при этом противник Фрейда, – составлял социограммы, изучая взаимоотношения между девочками, малолетними преступницами, в исправительной школе в Гудзоне, штат Нью-Йорк. В его исследовании, опубликованном в 1933 году ^[129] под названием “Кто выживет?” (Who Shall Survive?), показывалось, что большой рост числа сбежавших из учреждения в 1932 году становится объяснимым, если знать, какое место занимали беглянки в школьной социальной сети симпатий и антипатий, имеющих как расовый, так и сексуальный характер (см. вкл. № 2). Вот здесь, заявил Морено, и скрыты “общественные силы, которые господствуют над человечеством”. Его книга, считал он, станет “новой настольной книгой – руководством по социальному поведению, по человеческим сообществам” ^[130].

Спустя еще тридцать лет лингвист и библиограф Юджин Гарфилд придумал сходный графический способ наглядно показывать историю разных научных областей при помощи “историограммы” цитат. С тех пор индексы цитирования и “факторы влияния” стали стандартными инструментами измерения академических достижений в науке. А еще они дают возможность отображать процесс появления новых научных идей – например обнаруживая “невидимые колледжи”, которые вызываются к жизни сетями цитирования и которые весьма отличаются от тех настоящих колледжей, где работают большинство ученых ^[131]. Впрочем, подобные показатели иногда говорят лишь о том, что ученые склонны цитировать труды тех ученых, кто близок им по взглядам. Как гласит старая пословица, свой своему поневоле брат. Это относится не только к цитированию, но и ко многому другому. Если два узла связаны с третьим, то высока вероятность, что они окажутся связаны и друг с другом, потому что (говоря словами экономиста Джеймса Э. Рауха) “два человека, которые знакомы со мной, будут знакомы между собой с большей вероятностью, чем два произвольно выбранных человека” ^[132]. Триада, все участники которой связаны между собой положительными чувствами, называется “уравновешенной” и иллюстрирует изречение “друг моего друга – мой друг”. Другая триада, два участника которой не знают друг друга, хотя знают третьего участника, иногда называется “запретной триадой”. (Вариант, при котором два участника дружны между собой, а третий враждебен одному из них, являет собой пример такой неприятной ситуации, когда “враг моего друга – мой друг” ^[133].)

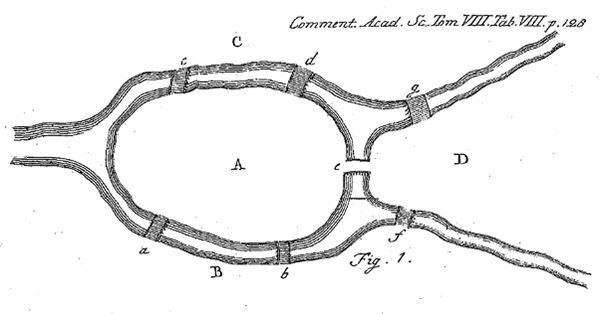
Илл. 4. Иллюстрация № 1 Эйлера из его книги Solutio problematis ad geometriam situs pertinentis [лат. “Решение задачи, связанной с геометрией положения”] (1741). Те, кто пожелал бы испытать решение задачи на месте, уже не имеют возможности сделать это, так как два из семи старинных мостов не пережили бомбежек города во время Второй мировой войны, а еще два были разрушены уже после того, как Кёнигсберг стал советским Калининградом.