Маленькая книга о черных дырах - Франс Преториус Страница 9

Из эксперимента Паунда – Ребки мы уже начинаем догадываться, почему гравитационное красное смещение имеет какое-то отношение к гравитационному притяжению. Для того чтобы это окончательно стало понятно, нам понадобится вспомнить еще об одном озарении Эйнштейна (в этом случае он следовал идеям Макса Планка): энергия фотона пропорциональна его частоте, так что когда частота уменьшается, уменьшается и энергия. Понятно, почему энергия фотона уменьшается, когда он летит вверх, – ведь при этом он преодолевает силу тяготения. Потеря энергии не может выражаться в замедлении фотона – в общей теории относительности, так же как и в специальной, свет всегда должен распространяться с одной и той же скоростью. И вместо замедления потеря энергии выражается в гравитационном красном смещении частоты фотона.

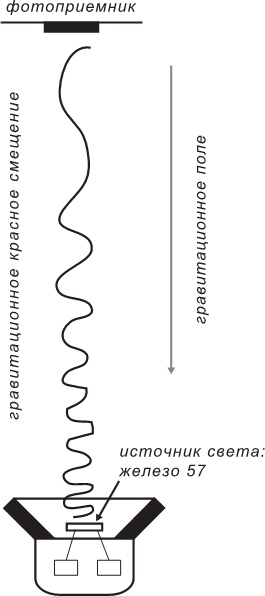
Рис. 2.2. Схема опыта Паунда – Ребки. Фотоны, испускаемые железом-57, летят вверх, преодолевая силу тяготения.

Наверху фотоприемник измеряет их гравитационное красное смещение.

Увеличение длины волны соответствует покраснению света.

Красное смещение в реальном эксперименте было гораздо меньше, чем показано на рисунке.

Из того, что мы узнали о замедлении времени в главе 1, мы могли бы подумать, что гравитационное красное смещение возникает по другой причине: при падении в гравитационный колодец все тела испытывают ускорение, а значит, их время замедляется. Но нет. Гравитационное красное смещение – нечто совсем другое, нечто совершенно новое. Ведь часы Паунда и Ребки покоились относительно Земли.

Гравитационное красное смещение происходит повсюду. Например, из-за него ваша голова стареет быстрее, чем пятки, – если, конечно, вы целыми днями не лежите на диване. Как и замедление времени, этот эффект численно очень мал и не сказывается на нашем ежедневном опыте: за время вашей жизни разница в возрасте головы и пяток составит несколько десятых долей микросекунды. Чтобы этот эффект стал более ярко выраженным, вам пришлось бы попасть в гораздо более сильное гравитационное поле, чем у Земли! Вот если бы при своих размерах Земля была бы черной дырой, а ваши пятки располагались бы всего в нескольких сантиметрах над ее горизонтом событий, вот тогда ваши пятки старились бы гораздо медленнее, чем голова, расположенная в метре над горизонтом. Конечно, опыт пребывания в такой среде был бы в буквальном смысле слова сногсшибательным. Но не забудем, что мы обсуждаем только абстрактную возможность.

Как включить идею о том, что тяготение обусловлено замедлением времени вблизи массивных тел, в описание обычных гравитационных явлений, таких как падение яблока или орбитальное движение планет? Для этого лучше всего подойдет высказывание, которое Вольтер вложил в уста своего Панглосса: «Все к лучшему в этом лучшем из миров». Во времена Вольтера ученые и математики, среди которых первым надо назвать Жозефа Луи Лагранжа, были убеждены, что движения массивных тел – падающих яблок и летящих по своим орбитам небесных тел – в некотором смысле происходят наилучшим возможным образом. Другими словами, постепенно ускоряющийся полет яблока с ветки к земле является как бы лучшим из всех возможных движений между исходным и конечным состояниями яблока. Великим достижением Лагранжа было то, что он сформулировал эту идею в точных математических терминах. В его описании любое представимое движение яблока между заданными начальным и конечным состояниями выражается через идею действия. Реальный способ движения, который «выбирает» яблоко, соответствует такому, при котором действие оказывается либо наименьшим, либо наибольшим. В любом случае действительное движение является лучшим в точно определенном математическом смысле.

Но для последователя Ньютона данное Лагранжем определение механики как задачи оптимизации покажется полным абсурдом. Как может неодушевленный объект «выбирать» оптимальный путь движения из множества возможных? По Ньютону, мир устроен совершенно иначе: предметы движутся по прямым линиям, пока на них не подействует сила, после чего их состояние движения изменяется в соответствии с законом F = ma. При чем же тут какая-то «оптимальность»? Но магия в том, что очень тщательно сконструировав для движущихся тел концепцию «действия», Лагранж сумел в точности воспроизвести законы Ньютона: ни больше, ни меньше. Да, надо признать, что выбор этой концепции был несколько парадоксальным. Но как только мы переходим к общей теории относительности, значение введенной Лагранжем формулировки становится очевидным. «Действием» объекта становится время, протекшее для наблюдателя, движущегося вместе с объектом. Движение, в действительности совершаемое объектом, оптимизирует собственное время, протекающее для этого объекта. Это принцип оптимального собственного времени. В случаях, которые мы будем рассматривать, собственное время максимально.

Один пример из специальной теории относительности поможет нам уточнить предмет нашего обсуждения.

(Не забудем, что в специальной теории относительности мы временно забываем о тяготении.) Этот пример называется парадоксом близнецов. Вот как он формулируется. У двух наблюдателей, которых мы, как обычно, назовем Алисой и Бобом, имеются совершенно одинаковые часы с секундомером. У Алисы есть звездолет и следующий план: она собирается улететь на нем от Боба на один день, двигаясь с постоянной скоростью (для определенности, равной половине скорости света), затем развернуться и возвратиться к Бобу. Боб тем временем останется на месте и не будет делать ничего. Если мы вспомним наше обсуждение собственного времени из главы 1, то сможем предвидеть результат этого эксперимента: длительность этого путешествия, измеренная Бобом по его часам, будет больше тех двух дней, которые пройдут для Алисы по ее часам. Точнее, при тех количественных данных, которые мы приняли, измеренное Бобом время путешествия Алисы составит примерно 2,3 дня.

Парадокс близнецов возникает вследствие следующего неверного рассуждения. Все движения относительны. Поэтому, с точки зрения Алисы, именно Боб улетел от нее, а потом вернулся. Разве она не должна точно так же, как и он, ожидать, что измеренное им время окажется меньше, чем по ее часам?

Чтобы увидеть, в чем недостаток этого рассуждения, нам следует точно определить различие между Алисой и Бобом: оно состоит в том, что Алиса испытала ускорение, когда разворачивалась, чтобы отправиться в обратный путь, а Боб этого не делал. Например, мы могли позволить Бобу свободно парить в пустоте в течение всего времени путешествия Алисы. С точки зрения Лагранжа, именно поведение Боба было «оптимальным», так как оно было абсолютно естественным и не требовало никакого внешнего вмешательства. Значит, то, что именно его собственное время оказалось большим, оправданно.

Есть замечательный вариант парадокса близнецов, в котором учитываются гравитационные эффекты (рис. 2.3). Допустим, что Алиса и Боб живут в глубоком гравитационном колодце, где они оба ходят в школу. У них трудное домашнее задание, которое им надо сдать через 48 часов, например, в 9:00 утра в понедельник. Из своего опыта с парадоксом близнецов Боб заключает, что больше всего времени на выполнение задания у него будет, если он станет как можно меньше двигаться. Поэтому он идет в школу очень медленным и спокойным шагом, все это время работая над своим заданием, и приходит туда в понедельник к 9:00 утра. Беспокойная Алиса соображает, что ей лучше прыгнуть в свою ракету и поскорее вылететь из гравитационного колодца: ведь отсутствие гравитационного красного смещения даст ей больше времени на выполнение задания. Но она опасается, что замедление времени, которое она испытает при полетах вверх и вниз, окажется более значительным. Согласно принципу оптимального собственного времени, чтобы максимизировать свое время, Алисе следует делать то, что при этих обстоятельствах делала бы инертная материя. А каково естественное поведение инертной материи? Она, как известно, любит покой! Получается, что план Боба минимизировать свои движения и идти в школу очень медленно правильный? Но все меняет присутствие тяготения. Вещество в гравитационном колодце вовсе не любит покоиться. Ему больше нравится падать. В присутствии тяготения для Боба вовсе не будет естественным тащиться в школу еле-еле: он может так поступать, только если находится на вершине какой-нибудь кучи вещества, которая в гравитационном колодце лежит еще глубже него. Если мы хотим, чтобы кусок инертного вещества отправился от дома Боба и Алисы в 9:00 утра в субботу и спустя 48 часов оказался бы у их школы, мы должны его запустить по изогнутой дугой траектории, чтобы ровно в 9:00 утра в понедельник он приземлился у школы. Сообразив все это, довольная Алиса залезает в свою ракету, жмет на газ, отчего ее ракета получает мощный импульс, на который уходит весь запас горючего, и весь остаток выходных летит по инерции, по дороге усердно работая над своим заданием^[3]. Ее ракета теперь не более чем баллистический снаряд, то есть, если не считать начального импульса на старте, она движется под действием только одной силы тяготения. Другими словами, она находится в состоянии свободного падения.