О том, чего мы не можем знать. Путешествие к рубежам знаний - Маркус Дю Сотой Страница 8
О том, чего мы не можем знать. Путешествие к рубежам знаний - Маркус Дю Сотой читать онлайн бесплатно
Ознакомительный фрагмент
Однако другие не были готовы признать свое поражение. Они обратили внимание не на прошлое, а на то, что могло бы случиться в будущем. В противоположность первой задаче здесь они попытались не предсказать, как ляжет кость, а представить все возможные варианты будущего и разделить выигрыш в соответствии с разными исходами, благоприятными для того или другого игрока.
Здесь легко впасть в заблуждение. Кажется, что существует три сценария. Если следующую партию выигрывает Ферма, он забирает себе все 64 фунта. Если следующую партию выигрывает Паскаль, то играется еще одна, финальная партия, которую может выиграть либо Паскаль, либо Ферма. Поскольку в двух из этих трех случаев выигрывает Ферма, то, видимо, ему причитаются две трети ставки. В эту-то ловушку и попал де Мере. Паскаль утверждает, что это решение ложно: «Кавалер де Мере – человек очень остроумный, но он вовсе не математик; это, как вы знаете, огромный недостаток» [15]. Вот уж действительно!
Паскаль же, напротив, был великий математик, и он считал, что выигрыш следует разделить иначе. Ферма может выиграть в следующей партии (и получить 64 фунта) с вероятностью 50 %. Но, если в следующей партии выиграет Паскаль, шансы обоих на победу в финальной партии равны, так что выигрыш можно разделить поровну – по 32 фунта каждому. Ферма в любом случае гарантированно получает 32 фунта. Поэтому оставшиеся 32 фунта следует разделить поровну, что в итоге дает Ферма 48 фунтов.
Ферма согласился с анализом Паскаля. «Я ясно вижу, что истина, будь она в Тулузе или в Париже, одна и та же», – писал ему в Тулузу Паскаль.
Анализ ставок в игре, разработанный Паскалем и Ферма, можно применить и к гораздо более сложным ситуациям. Паскаль выяснил, что тайна распределения выигрыша сокрыта внутри того, что теперь называют треугольником Паскаля.
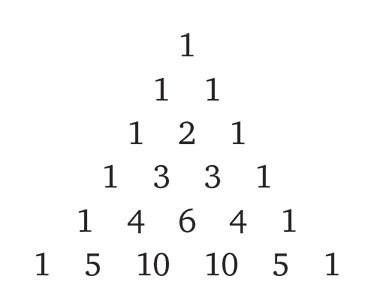
Треугольник устроен таким образом, что каждое число в нем равно сумме двух чисел, расположенных непосредственно над ним. Полученные числа определяют, как следует разделить выигрыш в любой прерванной игре. Например, если Ферма до победы не хватает двух выигранных партий, а Паскалю – четырех, нужно взять строку треугольника номер 2 + 4 = 6 и найти сумму первых четырех чисел и сумму последних двух. Эти суммы дают пропорцию, в которой следует разделить выигрыш. В данном случае получается пропорция 1 + 5 + 10 + 10 = 26 к 1 + 5 = 6. Таким образом, Ферма получает 26/32 · 64 = 52 фунта, а Паскаль – 6/32 · 64 = 12 фунтов. В общем случае решение для игры, в которой Ферма не хватает n, а Паскалю – m выигранных партий, можно найти в (n + m) – й строке треугольника Паскаля.
Есть данные, что французы опоздали с открытием связи между этим треугольником и исходом азартных игр на несколько тысячелетий. Игральные кости и другие методы получения случайных результатов, например «И цзин», издавна использовали в Китае в попытках предсказать будущее. В тексте книги «И цзин», созданном около 3000 лет назад, для случайного выбора гексаграммы, значение которой затем можно истолковать, используется в точности та же таблица, которую Паскаль составил для анализа исходов подбрасывания монет. Однако создателем треугольника считают в наше время Паскаля, а не китайцев.
Паскаль интересовался не только игральными костями. Он предпринял знаменитую попытку приложения своей новой вероятностной математики к величайшему из неизвестных – существованию Бога.
Бог есть или Бога нет. Но на которую сторону мы склонимся? Разум тут ничего решить не может. Нас разделяет бесконечный хаос. На краю этого бесконечного расстояния разыгрывается игра, исход которой неизвестен. […] На чем же вы остановитесь? Так как выбор сделать необходимо, то посмотрим, что представляет для вас меньше интереса: вы можете проиграть две вещи, истину и благо, и две вещи вам приходится ставить на карту, ваши разум и волю, ваше познание и ваше блаженство; природа же ваша должна избегать двух вещей: ошибки и бедствия. Раз выбирать необходимо, то ваш разум не потерпит ущерба ни при том, ни при другом выборе. Это бесспорно; ну а ваше блаженство? Взвесим выигрыш и проигрыш, ставя на то, что Бог есть. Возьмем два случая: если выиграете, вы выиграете все; если проиграете, то не потеряете ничего. Поэтому не колеблясь ставьте на то, что Он есть [16].
В этом рассуждении, известном под названием «пари Паскаля», он утверждает, что выбор веры в Бога приносит гораздо больший выигрыш. Если такой выбор ошибочен, вы ничего не теряете; если он справедлив, вы выигрываете вечную жизнь. И вместе с тем ставка на то, что Бога нет, в случае проигрыша приносит вечное проклятие, а в случае выигрыша не дает ничего, кроме знания, что Бога действительно нет. Этот аргумент рассыпается, если вероятность существования Бога на самом деле равна нулю, но, даже если это и не так, цена верования может оказаться слишком высокой по сравнению с вероятностью существования Бога.
Вероятностные методы, разработанные математиками, подобными Ферма и Паскалю, для разрешения неопределенности, оказались невероятно могущественными. Явления, считавшиеся недоступными для познания, выражением воли богов, начали становиться досягаемыми для человеческого разума. На сегодня такие вероятностные подходы являются лучшим из имеющихся у нас средств исследования буквально всего, от поведения частиц газа до подъемов и падений рынка ценных бумаг. Действительно, кажется, что сама природа материи отдана на милость математической вероятности, как мы увидим на «Рубеже третьем», говоря об использовании квантовой физики для предсказания поведения наблюдаемых нами частиц. Но с точки зрения поисков определенности такие вероятностные методы представляют собой раздражающий компромисс.
Я, безусловно, ценю величайшие открытия, сделанные Ферма, Паскалем и другими, но они не помогают мне узнать заранее, сколько очков выпадет на брошенной мной кости. Сколько я ни изучал математическую теорию вероятностей, меня никогда не покидало чувство неудовлетворенности. Единственное, что вбивает в голову любой курс теории вероятностей, – это идея о том, что, сколько бы раз подряд у вас ни выпадала шестерка, это никак не влияет на поведение кости при следующем броске.
Так можно ли как-нибудь узнать, как упадет моя кость? Или же это знание навечно останется недоступным? Не останется, если верить откровениям одного ученого, жившего за морем, в Англии.
Для меня Исаак Ньютон – главный герой борьбы с непознаваемым. Идея о том, что я могу узнать о Вселенной все, происходит из революционной работы Ньютона «Математические начала натуральной философии». Эта книга, впервые изданная в 1687 г., посвящена разработке нового математического языка, обещавшего дать инструменты, которые откроют секреты устройства Вселенной. В ней была предложена разительно новая модель занятий наукой. Как заявил в 1747 г. французский физик Алексис Клеро, эта работа «пролила свет математики на науку, которая до тех пор оставалась во тьме догадок и гипотез».
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии