Кому нужна математика? Понятная книга о том, как устроен цифровой мир - Андрей Райгородский Страница 6

Как получена заштрихованная область на рис. 2.1

Все значения АЮ и БЮ положительные.

Вертикальная прямая линия АЮ = 60 обеспечивает ограничение АЮ ≤ 60. Все возможные значения находятся либо на ней, либо слева от нее.

Аналогично горизонтальная прямая линия БЮ = 40 обеспечивает ограничение БЮ ≤ 40. Все возможные значения находятся либо на ней, либо под ней. Выражение штрихпунктирной прямой АЮ + БЮ = 70 можно переписать в более привычном виде:

БЮ = 70 − АЮ,

поэтому прямая идет под отрицательным углом 45°. Заметьте, что она пересекает ось х (в нашем случае ось АЮ), когда БЮ = 0 и, соответственно, АЮ = 70. Нам нужно, чтобы выполнялось неравенство АЮ + БЮ ≤ 70, то есть

БЮ ≤ 70 − АЮ.

Значения, удовлетворяющие этому неравенству, расположены на штрихпунктирной прямой или под ней.

Аналогично пунктирная прямая АЮ + БЮ = 65 обеспечивает ограничение АЮ + БЮ ≥ 65. Значения, которые удовлетворяют этому неравенству, находятся на этой прямой или над ней.

Заштрихованная область, включая границы, удовлетворяет всем ограничениям.

Важно отметить, что заштрихованная область – это четырехугольник с прямыми сторонами, поскольку все наши ограничения линейные, то есть их можно изобразить с помощью прямых линий. Данная область называется областью допустимых значений, потому что все значения в ней удовлетворяют всем ограничениям. Иначе говоря, любое решение из этой области физически возможно или допустимо.

Фундаментальное свойство задач линейного программирования заключается в том, что оптимальное решение обязательно находится в углах области допустимых значений. Это происходит потому, что наша стоимость тоже линейная. Когда мы движемся по прямой – горизонтальной, вертикальной или наклонной, – стоимость может либо только уменьшаться, либо только увеличиваться, пока мы не наткнемся на угол и идти дальше по той же прямой станет невозможно.

Для подготовленного читателя в приложении в конце книги мы приводим более формальное обоснование того, почему оптимальное решение задачи линейного программирования обязательно найдется в одном из углов области допустимых значений.

В нашем маленьком примере углов всего четыре: (25,40), (30,40), (60,10) и (60,5). Мы можем легко подставить значения и подсчитать, что самое лучшее решение в точке (30,40), то есть с южного склада нужно отправить 30 листов клиенту А и 40 листов клиенту Б. Оставшиеся 30 листов клиенту А следует отправить с северного склада. Результат приведен в табл. 2.3:

Таблица 2.3. Оптимальный план поставки листов железа

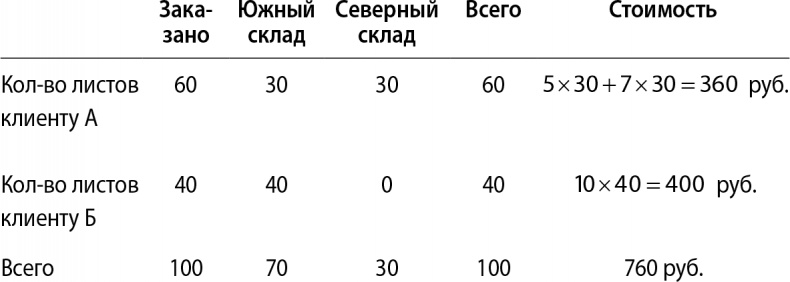
Общая стоимость – 760 рублей, что гораздо меньше, чем 864 рубля – наше первое, выбранное наобум решение. Выгода – 12 %, и это очень существенно, особенно если таких доставок много.

То, что решение нужно искать «по углам», сказано уже на первой странице работы Канторовича. Это понятно любому математику.

Если же ограничений много, то у нас получается уже не четырехугольник, а многоугольник. А если много переменных, у нас будет не многоугольник, а многогранник! Найти и перебрать все углы многогранника невероятно сложно, на это может уйти очень много времени.

Заслуга Данцига состоит в том, что он придумал способ, основанный на линейной алгебре, который позволяет перемещаться от одного угла многогранника к другому не наобум, а в определенном порядке, чтобы при переходе от одного угла к другому стоимость только уменьшалась. Это и есть знаменитый симплекс-метод, применяемый практически во всех приложениях. Доказано, что в самых худших случаях искать решение придется очень долго. Тем не менее на практике симплекс-метод в его современных вариантах быстро находит оптимальное решение.