Логика случая. О природе и происхождении биологической эволюции - Евгений Кунин Страница 6
Логика случая. О природе и происхождении биологической эволюции - Евгений Кунин читать онлайн бесплатно
Ознакомительный фрагмент
Нет ни надобности, ни практической возможности излагать здесь основы популяционной генетики [10]. Можно, однако, лаконично представить некоторые обобщения, имеющие отношение к остальной части обсуждения современной эволюционной биологии. Пусть и поверхностное, но такое резюме здесь будет существенно. По сути, основатели популяционной генетики осознали простой факт, что эволюция не действует на изолированные организмы или абстрактные виды, а направлена на конкретные группы скрещивающихся особей, называемые популяциями. Размер и структура эволюционирующей популяции в большой степени определяют направление и результат эволюции. В частности, Фишер сформулировал и доказал фундаментальную теорему естественного отбора (известную как теорема Фишера), в которой утверждается, что интенсивность отбора (и, следовательно, скорость эволюции путем отбора) пропорциональна величине генетической дисперсии по приспособленности эволюционирующей популяции, которая, в свою очередь, пропорциональна эффективному размеру популяции.
В табл. 1-1 собраны основные определения и уравнения, описывающие эффекты мутаций и давления отбора на устранение или закрепление мутантных аллелей в зависимости от эффективного размера популяции. Качественная суть этих уравнений в том, что при одинаковой скорости мутаций в популяции большего эффективного размера отбор более интенсивный. В таких популяциях даже мутации с небольшим положительным коэффициентом отбора («слегка» благоприятные мутации) закрепляются быстро. С другой стороны, мутации даже с очень маленьким отрицательным коэффициентом селекции («слегка» вредные мутации) быстро устраняются. Данный эффект был строго сформулирован в теореме Фишера.
Таблица 1-1
Фундаментальное соотношение, описывающее роль отбора и генетический дрейф в эволюции популяции
Почти нейтральная эволюция, управляемая дрейфом
1/Ne ≫ |s|
Эволюция, управляемая отбором
1/Ne ≪ |s|
Комбинированный режим, при сравнимом вкладе дрейфа и отбора
1/Ne ≈ |s|
Ne: эффективный размер популяции (как правило, значительно меньше, чем общее количество особей в популяции, так как не все особи могут дать жизнеспособное потомство)
s: коэффициент отбора, или влияние мутации на приспособленность:
s = FA – Fa
FA, Fa: величина приспособленности каждого из двух аллелей гена
s > 0: полезная мутация
s < 0: вредная мутация
Из теоремы Фишера следует, что при эволюции, направляемой только естественным отбором, средняя приспособленность популяции не может уменьшаться (если, конечно, популяция собирается выжить). Пожалуй, наилучшим образом это можно представить с помощью образа «адаптивного ландшафта», который впервые был предложен другим отцом-основателем популяционной генетики, Сьюэлом Райтом. Райт создал этот чрезвычайно удачный образ в ответ на просьбу своего научного руководителя представить результаты математического анализа отбора в приемлемой для биологов форме. Благодаря своей простоте и изяществу это представление адаптивной эволюции сохраняет свою ценность по сей день и стимулировало многочисленные исследования, в результате которых появились более сложные и менее интуитивно понятные адаптивные ландшафты, в том числе и многомерные (Gavrilets, 2004) [11]. В соответствии с теоремой Фишера популяция, эволюция которой идет только за счет отбора (строго говоря, популяция бесконечного размера — такие популяции, естественно, не существуют, но являются удобной абстракцией, часто используемой в популяционной генетике), никогда не будет двигаться вниз по адаптивному ландшафту (см. рис. 1-1). Легко представить, что адаптивный ландшафт, как и обычный ландшафт, может иметь самую различную форму. При определенных обстоятельствах ландшафт может быть очень гладким, с единственным пиком, соответствующим глобальному адаптивному максимуму (иногда такой ландшафт образно называют «гора Фудзияма» (см. рис. 1-1а). Реальный ландшафт, однако, неровный и содержит многочисленные пики различной высоты, разделенные долинами (см. рис. 1-1б). Формально, согласно теореме Фишера (и в целом, в соответствии с теорией Дарвина), популяция, эволюционирующая с помощью отбора, может только подниматься вверх и, таким образом, достигнуть только локального пика, даже если его высота значительно меньше, чем высота глобального пика (см. рис. 1-1а). Теория Дарвина и СТЭ утверждают, что движение популяции через долины запрещено, так как неизбежно подразумевает фазу спуска. Однако развитие популяционной генетики и ее применение к эволюционным процессам изменило эту упорядоченную картину, привнеся в нее понятие «дрейфа генов», ключевую идею эволюционной биологии, которую также предложил Райт.
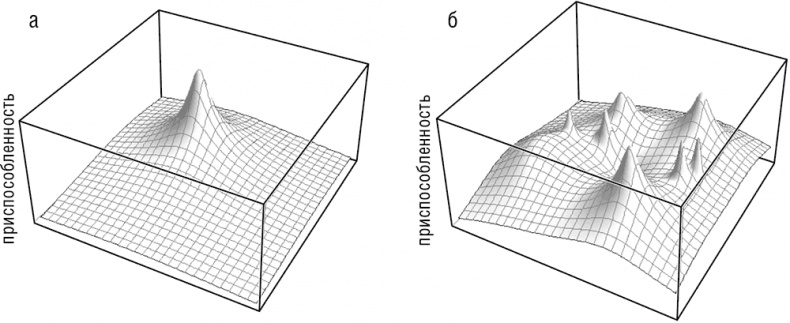
Рис. 1-1. Адаптивные ландшафты: а — «гора Фудзияма» с единственным (глобальным) пиком; б — «пересеченная местность» неровного адаптивного ландшафта.
Как подчеркивалось ранее, Дарвин признавал важную роль случайности в эволюции, но эта роль была ограничена только одной частью эволюционного процесса: появлением изменений (в современной терминологии — мутаций). В остальном эволюция рассматривалась как строго детерминистский процесс, где отбором закрепляются выгодные мутации, а все прочие мутации устраняются без какого-либо вреда для дальнейшего существования популяции. Однако при рассмотрении популяции в динамике картина значительно меняется. Основатели количественной популяционной генетики отразили в простых формулах зависимость интенсивности отбора от размера популяции и частоты мутаций (см. табл. 1-1 и рис. 1-2). Отбор эффективен в большой популяции, и мутация, несущая незначительное преимущество, почти наверняка закрепится (в популяции бесконечного размера закрепляется мутация с бесконечно малым положительным коэффициентом отбора). Райт понял, что в малой популяции, особенно при низкой частоте мутаций, эволюционный процесс идет по-другому. В такой популяции решающую роль играет дрейф генов, с помощью которого случайным образом часто закрепляются нейтральные и даже вредные (но, конечно, не летальные) мутации. Очевидно, с помощью генетического дрейфа эволюционирующая популяция может избежать однонаправленного подъема по адаптивному ландшафту и может спускаться (см. рис. 1-2) [12]. Преимущественно это выражается в движении вниз и последующем вымирании, однако если долина, отделяющая один локальный пик от другого, возможно даже более высокого, достаточно узкая, становится возможным переход через нее и последующее восхождение на более высокую вершину (см. рис. 1-2). Введение понятия генетического дрейфа в изучение эволюции является центральным в моем рассказе. Это новый уровень проявления случая. Хотя Дарвин и его ближайшие последователи видели роль случая в появлении наследуемых изменений (мутаций), дрейф вводит случайность на следующей стадии, то есть при закреплении этих изменений, забирая у отбора часть ответственности. В этой книге я исследую, насколько значимой может быть роль дрейфа в различных ситуациях в ходе эволюции.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.




Комментарии