Идеальная ставка - Адам Кучарски Страница 6
Идеальная ставка - Адам Кучарски читать онлайн бесплатно
Ознакомительный фрагмент
Проект начался в конце 1975 года, когда два выпускника Калифорнийского университета, Дуэйн Фармер и Норман Пэкард, купили подержанное «чертово колесо». Все предыдущее лето эти двое развлекались, испытывая разные беттинг-стратегии на всевозможных азартных играх, пока наконец не остановили свой выбор на рулетке. Несмотря на предостережения Шеннона, Торп все же намекнул в одной из своих книг, что способ переиграть рулетку существует. Одного этого невзначай оброненного на последних страницах книги замечания хватило, чтобы убедить Фармера и Пэкарда серьезно заняться «чертовым колесом». Работая по ночам в университетской лаборатории, они шаг за шагом вникали в особенности физики вращения рулетки. Внимательно наблюдая за крутящимся шариком и производя расчеты, они вскоре пришли к выводу, что полученной информации достаточно для того, чтобы делать выгодные ставки.
Один из эвдемонистов, Томас Басс, позже запечатлел их похождения в своей книге «Эвдемонический пирог». Он подробно описал, как, хорошенько все просчитав, участники группы спрятали компьютер в ботинке и с его помощью смогли предсказать движение шарика в нескольких казино. Однако Басс умолчал о самом важном – об уравнении, лежавшем в основе метода эвдемонистов.
Об эвдемонистах так или иначе слышали почти все математики, интересующиеся азартными играми. Многие к тому же задавались вопросом: а нельзя ли проверить легенду на практике? И когда в 2012 году в журнале Chaos появилась статья, посвященная рулетке, стало ясно: человек, готовый это сделать, нашелся.
Майкл Смолл впервые прочитал «Эвдемонический пирог», когда работал в южноафриканском инвестиционном банке. Он не был игроком и не любил казино, однако идея компьютера в ботинке ему понравилась. Его диссертация была посвящена анализу нелинейных динамических систем, и рулетка отлично вписывалась в эту категорию. Десять лет спустя Смолл переехал в Азию, где стал работать в Гонконгском политехническом университете. Вместе с коллегой с инженерного факультета Чи Кун Цэ они решили, что разработка «рулеточного» компьютера может стать интересным научным проектом.
Может показаться странным, что ученым понадобилось так много времени для публичного тестирования давно известной стратегии игры в рулетку. Но ведь и добраться до заветного колеса было не так легко: средства на посещение казино в графе университетских расходов обычно не значатся, так что возможности для проведения исследовательской работы ограниченны. Пирсон полагался на ненадежные данные, полученные из газет, потому что не нашел спонсора, который оплатил бы ему поездку в Монте-Карло, а Торп вряд ли смог бы продолжить свои эксперименты без поддержки Шеннона.
Препятствовала исследованиям и математическая составляющая проблемы. И не потому, что управляющие рулеткой математические законы чересчур сложны, наоборот – они слишком просты. Редакторы научных журналов очень разборчивы в выборе публикаций, и попытки разобраться в поведении «чертова колеса» при помощи школьных знаний – тема не очень для них привлекательная. Впрочем, иногда в печати все же появлялись публикации, посвященные рулетке, например работа Торпа с описанием его метода. И хотя Торп разболтал достаточно, чтобы убедить читателей, в том числе эвдемонистов, что смоделированный на компьютере прогноз может быть успешным, подробности он опустил. Самые интересные вычисления в статье явно отсутствовали.
Уговорив руководство университета приобрести рулетку, Смолл и Цэ попытались воспроизвести стратегию эвдемонистов. Они начали с разделения траектории шарика на три фазы.
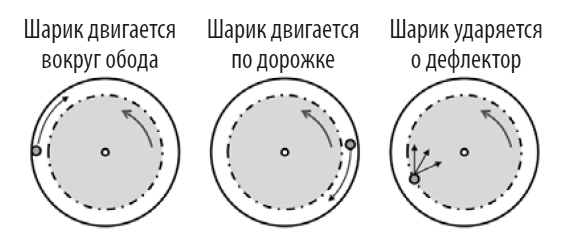
Три стадии спина
Когда крупье запускает колесо рулетки, шарик сначала двигается вокруг его верхнего обода, в то время как центральная часть рулетки крутится в противоположном направлении. В это время на шарик воздействуют две конкурирующие силы: центростремительная сила удерживает его на ободе, а сила притяжения тянет вниз, к центру колеса.
Ученые принимали во внимание, что во время вращения шарика сила трения замедляет его движение. В конце момент импульса шарика уменьшается настолько, что гравитация побеждает. В этой точке шарик переходит во вторую фазу – он сходит с ободка и беспрепятственно движется по дорожке между ободком и дефлекторами. Шарик постепенно смещается к центру колеса до тех пор, пока не столкнется с одним из расположенных на окружности дефлекторов.
До этой точки траекторию шарика может просчитать даже школьник. Но как только он ударяется о дефлектор, его траектория рассеивается, и теоретически он может остановиться в одной из нескольких ячеек. Для игроков это означает, что шарик покидает мир уютной предсказуемости и погружается в подлинный хаос.
С этой неопределенностью Смолл и Цэ могли справиться при помощи статистических измерений. Правда, для простоты они решили свести прогноз к определению числа на рулетке, рядом с которым будет находиться шарик, когда столкнется с дефлектором. Чтобы предсказать точку, в которой шарик будет задевать один из дефлекторов, Смоллу и Цэ необходимы были шесть параметров: первоначальное положение шарика, его скорость и ускорение и аналогичные показатели для рулетки. К счастью, эти шесть параметров можно было свести к трем, если рассматривать траекторию с другой отправной точки. Для стороннего наблюдателя шарик движется в одном направлении, а колесо – в другом. Однако расчеты можно произвести и «с позиции шарика», в этом случае необходимо только измерить, как шарик движется относительно колеса. Смолл и Цэ делали такие расчеты посредством секундомера, фиксируя время прохождения шариком определенной точки.
Написав компьютерную программу для проведения расчетов, Смолл приступил к экспериментальному тестированию системы. Он запустил шарик в рулетке, проводя необходимые измерения вручную, как это делали эвдемонисты. Когда шарик описал около дюжины кругов вдоль обода колеса, Смолл собрал достаточно информации, чтобы предугадать, где он остановится. В этот день он смог провести свой эксперимент 22 раза, прежде чем пришлось закрывать кабинет. Три попытки увенчались успехом – Смолл смог точно спрогнозировать число, на которое выпадет шарик. Если бы он брал случайные числа, вероятность получения такого результата (значение р) составила бы менее 2 %. Теперь Смолл не сомневался: стратегия эвдемонистов работает, и наука может победить рулетку.
После ручных измерений Смолл и Цэ установили высокоскоростную камеру для сбора более точных данных о положении шарика. Камера делала примерно 90 снимков в секунду, позволяя увидеть, что происходит с шариком после столкновения с дефлектором. С помощью двух студентов-инженеров ученые запустили колесо 700 раз, фиксируя разницу между своими прогнозами и полученным результатом. Собрав всю информацию, они рассчитали вероятность остановки шарика на определенном расстоянии от прогнозируемой ячейки. Для большинства ячеек эта вероятность не была особо малой или большой; выпадение было приблизительно таким же, как если бы они выбирали ячейки в этой области случайно. Тем не менее вырисовывалось несколько закономерностей. Шарик останавливался в прогнозируемой ячейке намного чаще, чем если бы его движение было хаотично. Более того, он редко останавливался на цифрах, расположенных непосредственно перед прогнозируемой ячейкой. Последнее, впрочем, было вполне объяснимо: чтобы добраться до этих ячеек, шарику пришлось бы отскакивать назад.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии