Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир Страница 46
Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир читать онлайн бесплатно
Таким образом, получаем
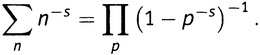
что я и назвал Золотым Ключом.
Пока все прекрасно, но что это там говорилось насчет нетривиальных нулей? Что такое нуль функции? Что представляют собой нули дзета-функции? И когда они нетривиальны? Не переживайте, сейчас все будет!
II.
Позабудем на время о дзета-функции. Рассмотрим бесконечную сумму совсем другого типа:
Сходится ли она вообще когда-нибудь? Без сомнения. Если x равно 1/2,то сумма представляет собой просто-напросто выражение 1.1 из главы 1.iv, поскольку (1/2)2 = 1/4, (1/2)3 = 1/8 и т.д. Следовательно, S(1/2) = 2, потому что именно к этому значению ряд и сходится. Более того, если вспомнить правило знаков, то (−1/2)2 = 1/4, (−1/2)3 = −1/8 и т.д., а следовательно, S(−1/2) = 2/3 согласно выражению 1.2 из главы 1.v. Аналогичным образом выражение 1.3 говорит нам, что S(1/3) = 11/2 выражение 1.4 — что S(−1/3) = 13/4. Легко получить и еще одно значение для этой функции: S(0) = 1, поскольку нуль в квадрате, кубе и т.д. все равно равен нулю, и остается только единица, с которой ряд начинается.
Однако если x равен 1, то S(1) есть 1 + 1 + 1 + 1 + …, а этот ряд расходится. При x равном 2 расходимость еще более явная: 1 + 2 + 4 + 8 + 16 + …. Когда x равен −1, происходит странная вещь: по правилу знаков сумма принимает вид 1 − 1 + 1 − 1 + 1 − 1 + …. Такая сумма равна нулю, если взять четное число членов, и единице, если нечетное. Данное выражение определенно не убегает на бесконечность, но оно и не сходится. Математики рассматривают такое поведение как некоторый вид расходимости. Ситуация с x = −2 еще хуже: сумма 1 − 2 + 4 − 8 + 16 − … ведет себя так, словно убегает на бесконечность сразу по двум направлениям. Такая ситуация определенно далека от сходимости, и если вы скажете, что здесь налицо расходимость, то никто с вами спорить не будет.
Короче говоря, функция S(x) имеет значения, только когда x лежит в границах между −1 и 1, не включая сами границы. В других случаях у нее значений нет. В таблице 9.1 приведены значения функции S(x) для аргументов x между −1 и 1.
| x | S(x) |
|---|---|
| −1 или меньше | (нет значений) |
| −0,5 | 0,6666… |
| −0,333… | 0,75 |
| 0 | 1 |
| 0,333… | 1,5 |
| 0,5 | 2 |
| 1 или больше | (нет значений) |
Таблица 9.1. Значения функции S(x) = 1 + x + x2 + x3 + ….
Вот и все, что можно извлечь из бесконечной суммы. График этой функции показан на рисунке 9.1; на этом графике у функции нет вообще никаких значений к западу от −1 и к востоку от 1. Используя профессиональную терминологию, можно сказать, что область определения этой функции заключена строго между −1 и 1.
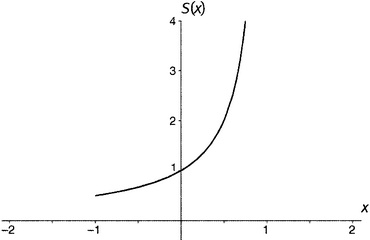
Рисунок 9.1. Функция S(x) = 1 + x + x2 + x3 + ….
III.
Но смотрите, нашу сумму
можно переписать в таком виде:
Ряд в скобках здесь равен просто S(x): каждый член, встречающийся в одном, встречается также и в другом из двух выписанных выше рядов, а это и означает, что они совпадают.
Другими словами, S(x) = 1 + xS(x). Перенося самый правый член в левую часть, получаем равенство S(x) − xS(x) = 1, или, другими словами, (1 − x)S(x) = 1. Следовательно, S(x) = 1/(1 − x). Возможно ли, чтобы за нашей бесконечной суммой скрывалась столь простая функция, как 1/(1 − x)? Может ли равенство
оказаться верным?
Без сомнения, может. Если, например, x = 1/2, то 1/(1 − x) равняется 1/(1 − 1/2), что есть 2. Если x = 0, то 1/(1 − x) равно 1/(1 − 0), что есть 1. Если x = −1/2, то 1/(1 − x) равняется 1/(1 − (−1/2)), т.е. 1:11/2 что есть 2/3. Если x = 1/3, то 1/(1 − x) равняется 1/(1 − 1/3) т.е. 1:2/3, что есть 11/2. Если x = −1/3, то 1/(1 − x) равняется 1/(1 − (−1/3)), т.е. 1:11/3, что есть 3/4. Все сходится. Для аргументов −1/2, −1/3, 0, 1/3, 1/2, при которых мы знаем значения функции, значения бесконечного ряда S(x) такие же, как и значения функции 1/(1 − x). Похоже, что этот ряд и эта функция — одно и то же.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии