Истина и красота. Всемирная история симметрии - Йен Стюарт Страница 31
Истина и красота. Всемирная история симметрии - Йен Стюарт читать онлайн бесплатно
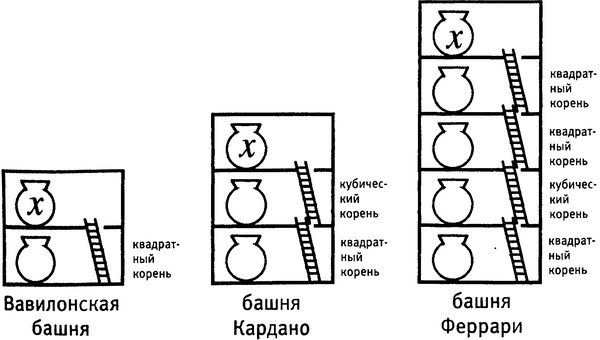
Решение квадрики, кубики и квартики.
Наконец мы добираемся до пятого этажа — чердака, — составляя безобидные комбинации и беря затем подходящий квадратный корень.
И вот — мешок на чердаке действительно содержит то, что мы искали, — некий корень уравнения четвертой степени. Формула Феррари снабжает нас инструкциями по построению именно нужной башни.
Вавилонская башня, которая решает уравнение второй степени, также подходит под эту метафору. Но она оказывается укороченной башней всего с двумя этажами. Мешок на первом этаже содержит просто комбинации коэффициентов. Единственный, тщательно выбранный квадратный корень ведет на один этаж выше — уже на чердак. Внутри этого мешка имеется корень квадратного уравнения — в действительности оба его корня. Об этом нам говорит вавилонская процедура решения квадратных уравнений — формула, которой нас учили в школе.
А что же насчет уравнения пятой степени?
Предположим, что формула для решения квинтики в радикалах на самом деле существует. Мы не знаем, как она выглядит, но тем не менее можем многое о ней сказать. В частности, она должна соответствовать некоторой башне. Назовем эту гипотетическую башню башней Абеля.
Зададимся вопросом, как забраться вверх по башне; математика говорит нам, что имеется только один способ подняться на второй этаж. Надо взять один определенный квадратный корень, другого пути наверх нет.
Впрочем, не совсем так. Мы могли бы брать всевозможные другие корни и построить огромную, высоченную башню. Но чтобы на чердаке такой башни находился корень, необходимо, чтобы некоторый этаж соответствовал тому самому определенному квадратному корню, который я имею в виду. И ни один из предыдущих этажей не поможет нам добраться до чердака; строительство будет лишь пустой тратой времени и денег. Так что любой вменяемый строитель обязательно начнет именно с этого квадратного корня.
Что требуется, чтобы подняться по лестнице на третий этаж?
На третий этаж лестницы нет. Можно забраться на второй этаж, но там мы и застрянем. И если нельзя подняться на третий этаж нашей воображаемой башни, то заведомо нельзя добраться до чердака и найти там в мешке корень.
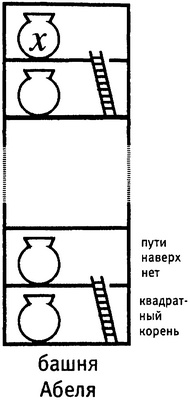
Почему уравнение пятой степени неразрешимо.
Одним словом, башни Абеля не существует. Все попытки прекращаются, когда мы упираемся в бетонный потолок на втором этаже; или, возможно, имеется некоторая более сложно организованная структура с множеством никому не нужных этажей, где мы в конце концов упираемся в бетон точно таким же образом и по той же самой причине. Это и доказал Руффини, если не считать одного технического пробела. Грубо говоря, он не сумел доказать, что если на чердаке живут безобидные комбинации радикалов, то и сами радикалы живут там же.
Доказательство Руффини и башня Абеля имеют выраженное сходство. Но, используя башни, Абель улучшил тактику Руффини и закрыл остававшуюся там дыру. Вместе они доказали, что нет никакой радикальной башни, позволяющей добраться от коэффициентов уравнения пятой степени к его корням. В переводе с архитектурного это значит, что нет формулы для корня уравнения пятой степени, сложность которой ограничивается радикалами. Решить уравнение пятой степени в радикалах невозможно, подобно тому как невозможно забраться на Луну, по очереди вставая друг другу на плечи.
Рождество 1828 года Абель планировал провести у своих старых друзей Катарины и Нильса Трешов во Фроланде. Он собирался навестить Крелли, жившую неподалеку. Абель не очень хорошо себя чувствовал, и его врач был против этой поездки. В письме к жене Кристофера Ханстеена Иоанне Катарина писала: «Если бы вы были в городе, он, пожалуй, согласился бы остаться. Но он старался скрыть, насколько серьезно он на самом деле болен». В середине декабря Абель направился во Фроланд, экипировавшись так, чтобы противостоять зимней стуже. Он прибыл туда 19 декабря, закутанный во всю наличествовавшую у него одежду, включая носки, которые он натянул на руки. Несмотря на приступы кашля и озноба, в математическом плане он мощно продвигался вперед; в доме Трешов ему нравилось работать в гостиной в окружении их детей. Он любил их общество.
Абель не оставлял попыток найти постоянное место работы. Даже его временная должность в Христиании была под вопросом. После Рождества он сосредоточил усилия на том, чтобы получить работу в Берлине. Посредством закулисной дипломатии его друг Август Крелле сумел убедить Отдел образования создать Математический институт и надеялся устроить дело таким образом, чтобы Абель стал там одним из профессоров. Он получил поддержку от такого научного светила, как Александр фон Гумбольдт, а также рекомендацию от Гаусса и еще одну от Адриена-Мари Лежандра, видного члена Французской академии. Крелле убеждал министра образования, что Абель будет рад занять должность в Берлине, но что действовать следует быстро, поскольку Абеля хотят пригласить и в другие места, в особенности в Копенгаген.
Абель собирался уехать из Фроланда в Осло 9 января, но приступы кашля и озноба усилились, и он проводил большую часть времени, оставаясь в своей комнате. Кемпы, его будущие родственники со стороны невесты, сильно обеспокоились. Утром того дня, когда он предполагал уехать, у Абеля начался очень сильный кашель с кровохарканьем. В дом немедленно вызвали семейного врача, и он прописал постельный режим и постоянный уход. Крелли стала исполнять роль медсестры, и ее заботливое внимание и различные лекарства привели к некоторому улучшению. В течение нескольких недель Абелю позволили недолгое время сидеть на стуле. Ему пришлось отказаться от всяких занятий математикой.
Лежандр написал Абелю письмо, в котором рассказывал, какое впечатление на него произвели работы норвежца по эллиптическим функциям, и побуждал молодого человека опубликовать свое решение задачи о том, когда уравнение можно решить в радикалах: «Я настаиваю на том, что эта новая теория должна появиться в печати как можно скорее. Она прославит вас и будет всегда и всеми рассматриваться как величайшее открытие, которое оставалось сделать в математике». В то время как некоторые видные математики противодействовали публикации основополагающих работ Абеля — одни сознательно, другие — просто не придавая им большого значения, — его репутация среди других ученых быстро набирала силу.
К концу февраля 1829 года врач Абеля понял, что надежды на выздоровление нет и что лучшее, что остается делать, — это по мере возможности сдерживать развитие болезни. Врач послал бывшему учителю Абеля Бернту Холмбоэ бюллетень о состоянии здоровья молодого человека:
…Вскоре после прибытия на Фроландский металлургический завод он стал страдать от тяжелого приступа пневмонии, сопровождавшегося значительным отхаркиванием, которое вскорости прекратилось… Однако хронический кашель и значительная слабость вынудили его оставаться в постели, и он по-прежнему должен соблюдать постельный режим; более того, ему нельзя подвергать себя воздействию малейших изменений в окружающей температуре.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии