Гейзенберг. Принцип неопределенности - Жозе Наварро Фаус Страница 3
Гейзенберг. Принцип неопределенности - Жозе Наварро Фаус читать онлайн бесплатно
С внезапной смертью заведующего кафедрой древнегреческого языка Мюнхенского университета жизнь Гейзенбергов изменилась. Как правило, при освобождении одной из существующих должностей или учреждении новой руководство университета обращалось к различным экспертам, в том числе зарубежным, и с их помощью составляло список из трех кандидатов, который подавался в министерство образования. Однако в этом случае должность требовалось занять как можно скорее, и министерству был представлен единственный кандидат, имевший прекрасные рекомендации. Таким образом, в начале 1910 года Август Гейзенберг возглавил единственную в Германии кафедру византийской филологии.
В одном из интервью 1960-х годов Вернер Гейзенберг упомянул два важных обстоятельства, в которых его отец сыграл значительную роль. Август был прекрасным учителем, он занимался с детьми в игровой форме и стремился поддерживать между ними дух соперничества. Часто отец предлагал старшему брату решать математические задачи, и юный Вернер, поняв, что ему это тоже по силам, почувствовал интерес к математике. Кроме этого, Август Гейзенберг прививал детям любовь к музыке. Вернер играл на виолончели и пианино и часто аккомпанировал отцу, когда тот пел тенором оперные арии. Эта игра на пианино и вообще увлечение музыкой сопровождали ученого всю его жизнь, и он достиг немалых высот для любителя.
Среднее образование
После образовательной реформы Гумбольдта, прошедшей в Германии в XIX веке, основной задачей гимназий стало гуманитарное образование, основанное на изучении древнегреческого и латыни. Считалось, что такое образование лучше всего воспитывает моральные и интеллектуальные качества будущей элиты общества. Гимназический аттестат был необходим для поступления в университет.
Хотя в начале XX века появились и другие образовательные учреждения, гимназии по-прежнему считались элитарными учебными заведениями, а преподаватели латыни и греческого пользовались большим авторитетом. Преподавать в гимназии эти дисциплины могли только лица, имеющие степень доктора, хотя от других преподавателей этого не требовалось.
В сентябре 1911 года Гейзенберг начал обучение в Максимилиановской гимназии, директором которой в то время был его дед. Гимназический курс состоял из девяти классов. Как правило, школьники учились в гимназии с 11 до 19 лет. Почти 40 % времени уделялось классическим языкам и литературе, 24 % – немецкому языку и математике. Остальное время распределялось между историей, религией, французским языком и рисованием. Физика преподавалась только в трех старших классах по два часа в неделю.
Я очень интересовался теоремой Ферма и, разумеется, как и все остальные, провел некоторое время в попытках доказать ее.
Гимназические преподаватели Гейзенберга всегда отмечали его исключительные знания. Вернер по праву считался одним из лучших учеников в своем классе и всегда имел высший балл по математике. Возможно, благодаря соперничеству с братом, которое поощрял отец мальчика, при поступлении в гимназию Вернер знал намного больше, чем требовалось. Неудивительно, что преподаватель математики предлагал ему в дополнение к обычным задачам другие, более сложные. Отец, видя интерес сына к математике, достал для него несколько книг… написанных на латыни, чтобы убить одним выстрелом двух зайцев. Должно быть, отец переоценивал возможности Вернера – вместе с другими книгами он передал ему докторскую диссертацию по теории чисел Леопольда Кронекера, опубликованную в 1845 году Конечно, Гейзенберг многое в этой работе не понял, но зато познакомился с простыми числами, критериями делимости, теоремой Ферма и так далее. В результате в 1916 году музыка и теория чисел стали основными интересами Вернера.
Магия целых чисел
В теории атомных спектров, на основе которой позднее была создана квантовая физика, основную роль играли именно целые числа. Однако сначала коротко расскажем о дискретности и непрерывности. Рассмотрим все десятичные дроби, целая часть которых равна нулю, например 0,73649100093. Существует бесконечное множество таких чисел, так как мы всегда можем добавлять к их записи все новые и новые знаки после запятой. Эти числа образуют непрерывное множество, так как для любых двух таких чисел можно найти третье число, заключенное между ними. Однако на этом бесконечном множестве можно выделить особые числовые ряды, например 1/2,1/3,1/4, 1/5 … или 1/22 , 1/32 , 1/42 , 1/52 … Эти ряды также будут содержать бесконечное множество членов, которые, однако, уже не будут образовывать непрерывного множества: к примеру, между 1/3 и 1/4 не заключено никакое число ряда. Говорят, что такие числа образуют дискретное множество. Теперь вернемся к атомным спектрам.
При прохождении солнечного света через призму образуется радуга. Каждый ее цвет характеризуется частотой или длиной волны. Эти величины связаны: произведение частоты на длину волны равно скорости распространения волны. Теперь рассмотрим нагретый светящийся газ, подобный тому, который можно увидеть в люминесцентных лампах. Если мы пропустим свет, излучаемый газом, через призму, то вместо радуги увидим несколько ярких линий, соответствующих определенным значениям частоты. Такой спектр называется дискретным. Кроме того, если пропустить через призму белый свет, который до этого прошел через газ, то на непрерывном спектре будут заметны темные линии, в точности соответствующие ярким линиям спектра этого же светящегося газа.
Спектры
Светящиеся газы испускают излучение, которое можно проанализировать с помощью спектрометра. Основным элементом этого устройства является призма. Все остальные его компоненты – шкалы, линзы и другие оптические приборы – служат для точного измерения длин волн в видимой, инфракрасной и ультрафиолетовой частях спектра. Как показано на рисунке 1, при прохождении белого света через призму образуется непрерывный спектр из всех цветов радуги. Если же через призму проходит свет, испускаемый светящимся газом, то будут видны лишь несколько ярких линий, соответствующих определенным значениям частоты. В таких случаях говорят о дискретном спектре. Кроме того, если пропустить через призму белый свет, который до этого прошел через газ, то на непрерывном спектре будут заметны темные линии, соответствующие линиям спектра этого же светящегося газа.
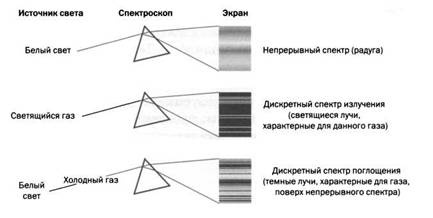
Рис. 1
На рисунке 2 показана часть спектра водорода и ртути. Длины волн заключены в интервале между 660 и 190 нм (нанометр – одна миллиардная часть метра). Видимый спектр соответствует диапазону частот 400- 700 нм. Чтобы найти частоты этих линий, нужно разделить скорость света (300000 км/с) на соответствующие длины волн. Результаты будут пропорциональны разности двух энергий. На заре атомной физики ученые стремились рассчитать величины этих энергий, которые зависели от определенных квантовых чисел, по известным разностям энергий. Вскоре стало очевидно, что получить все возможные разности энергий в ходе экспериментов нельзя. В результате были определены различные правила выбора, в которых фигурировали квантовые числа.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии