Популярная физика. От архимедова рычага до квантовой теории - Айзек Азимов Страница 24
Популярная физика. От архимедова рычага до квантовой теории - Айзек Азимов читать онлайн бесплатно
Если столкновение не было ни совершенно упругим, ни полностью неупругим, если шайбы отпрыгнули обособленно, но только слабо, то значение количества движения для каждой из шайб могло бы изменяться от mv до –0,2mv, в то время как количество движения другой шайбы могло измениться от –mv до 0,2mv. В любом случае конечная сумма была бы равна нулю.
Все это справедливо и в том случае, если шайбы встречаются «под углом», а не «лоб в лоб» и касаются друг друга «по скользящей». Если они встречаются «под углом», то есть таким образом, что их скорости не направлены в точно противоположных направлениях, оба импульса этих тел не обнулятся, даже если скорости этих двух шайб были равны. Полное количество движения системы можно вычислить векторным сложением этих двух индивидуальных импульсов. И шайбы тогда отпрыгнут таким образом, каким укажет вектор их суммы. Это же сложение укажет нам на тот факт, что суммарное общее количество движения системы осталось таким же, как до столкновения. Все это также справедливо для частного случая, когда двигающаяся шайба ударяет скользящим ударом в шайбу, находящуюся в состоянии покоя. Шайба, находящаяся в состоянии покоя, будет приведена в движение, а шайба, которая изначально перемещалась, изменит направление своего движения; однако оба получившихся в результате столкновения импульса в итоге составят величину, равную оригинальной.
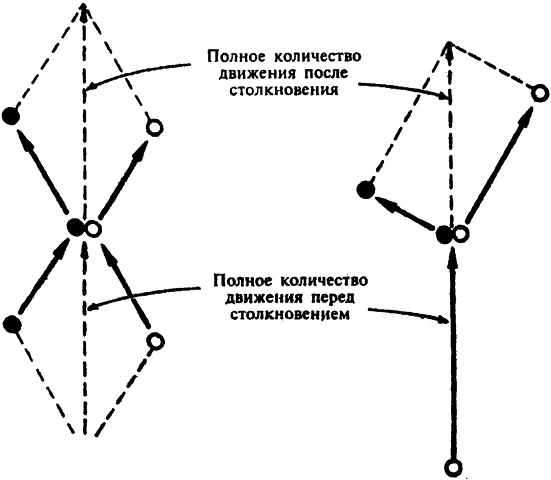
Сохранение количества движения
Рассматриваемые величины останутся, по существу, неизменными, даже если эти две шайбы имели различные массы. Предположим, что одна шайба перемещалась с некоторой данной скоростью направо и имела количество движения, равное mv, в то время как другая, имеющая массу в три раза больше первой, перемещалась с той же самой скоростью налево и имела поэтому импульс, равный –3/mv. Если рассмотреть эти две, связанные вместе после столкновения «лоб в лоб», объединенные шайбы (с полной массой 4 т), то мы увидим, что они продолжили бы перемещаться влево, в направлении, в котором двигалась более массивная шайба, но суммарная скорость системы была бы равна половине начальной скорости оригинала (— v/2). Первоначальное количество движения системы было: mv + (–3mv), или –2mv. Окончательное количество движения системы будет: (4m) x (–v/2), или –2mv. Опять мы видим, что полное количество движения системы осталось неизменным.
А что получается в том случае, если количество движения, как кажется, создано «из ничего»? Давайте рассмотрим пулю, которая первоначально находится в состоянии покоя (поэтому ее количество движения равно нулю), которую внезапно выстреливают из ружья, а значит — она начинает перемещаться с высокой скоростью. Как мы знаем, пуля теперь имеет значительное количество движения, равное (mv). Однако пуля — это только часть системы. Оставшаяся часть системы — ружье — тоже должно получить импульс, равный –mv, так как оно перемещается в противоположном направлении. Если ружье обладает массой в n раз большей, чем масса пули, оно должно переместиться в противоположном направлении со скоростью, равной 1/n скорости ускоряющейся пули. Количество движения ружья (минус пуля) будет тогда: (nm)∙(–v/n), или –mv. (Если в момент выстрела ружье не было закреплено, то этот «обратный» рывок его — хорошо виден. Если же мы стреляем из ружья обыкновенным образом, то чувствуем его обратное движение в виде «отдачи».) Полное количество движения, равное импульсу пули плюс импульс ружья, как было равно нулю до выстрела, так и осталось равно нулю после выстрела, хотя в данном случае распределение количества движения среди частей системы весьма различается до и после выстрела.
Короче говоря, все эксперименты, которые мы можем провести, приводят нас к заключению, что: «Полное количество движения изолированной системы тел остается постоянным». Это выражение называется законом сохранения импульса.
Конечно, чтобы доказать обобщение, нужно не просто перечислять отдельные случаи, подтверждающие его истинность. Независимо от того, насколько часто вы экспериментируете и приходите к выводу, что количество движения сохранено, вы не можете заявить с уверенностью, что так будет всегда. В лучшем случае можно заявить, что поскольку эксперимент за экспериментом подтверждают истинность закона и поскольку в результате экспериментов не было получено данных, опровергающих этот закон, то существует большая вероятность того, что данный закон верен. Было бы гораздо лучше, если бы мы могли доказать обобщение, опираясь на другое обобщение, истинность которого уже была доказана ранее.
Например, предположите, что дна тела любой массы, перемещающиеся с любыми скоростями, сталкиваются под любым углом, с любой степенью упругости. В момент столкновения одно тело прикладывает силу (f) ко второму. В соответствии с третьим законом Ньютона второе тело прикладывает к первому телу равную и противоположную по знаку силу (–f). Сила прикладывается в течение времени, пока эти два тела остаются в контакте. Время (t) контакта, очевидно, одинаково для обоих тел, поскольку, когда первое тело перестает быть в контакте со вторым, второе также перестает быть в контакте с первым. Это означает, что импульс первого тела на втором равен ft, а второго на первом равен –ft.
Импульс первого тела на втором передает изменение количества движения, равное mv, второму телу. Но импульс второго тела на первом, являющийся абсолютно равным по величине, но противоположным по знаку, должен передать изменение в количестве движения, равном –mv, первому. Изменения в количестве движения могут быть большие или маленькие в зависимости от размера импульса, угла столкновения и эластичности материала; однако независимо от величины изменения количества движения первого тела изменение количества движения второго тела равно по величине и противоположно по направлению. Полное количество движения системы должно оставаться тем же самым.
Таким образом, закон сохранения импульса может быть получен из ньютоновского третьего закона движения. На самом деле, однако, этого не произошло, и закон сохранения импульса был открыт в 1671 году английским математиком Джоном Валлисом (1616–1703) на дюжину лет раньше, чем Ньютон опубликовал свои законы движения. Обратный путь, кстати, тоже возможен, и третий закон движения тоже можно получить из закона сохранения импульса.
Туг у вас может появиться ощущение, что что-то не так, ведь если физики доказывают закон сохранения количества движения, опираясь на третий закон движения, а затем доказывают третий закон движения, исходя из закона сохранения количества движения, то они фактически ходят по кругу и не доказывают ничего вообще. Это бы и было, если бы происходило так, но все происходит иначе.
Здесь не столько вопрос «доказательства», сколько вопрос создания предположения и демонстрации последствий этого предположения. Можно начинать с того, что принять третий закон движения, а затем показать» что закон сохранения импульса есть следствие его действия. Точно так же можно начать с того, что принять закон сохранения импульса и показать, что третий закон — следствие из него.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии