Музыкальный инстинкт. Почему мы любим музыку - Филип Болл Страница 19

Этой системе в 1558 году придал официальный статус Джозеффо Царлино, хормейстер Собора святого Марка в Венеции. Он предложил следующую последовательность соотношений частот (здесь для до):

Система Царлино стала известна под названием «натуральный строй». Хотя ему удалось сохранить простые соотношения, возникли новые трудности. Небольшое смещение терции и сексты стало причиной появления двух разных шагов в «целый тон»: в одном две последующие ноты отличаются частотой на фактор 9/8 (здесь до-ре, фа-соль и ля-си), а в другом эта разница составила 10/9 (ре-ми, соль-ля). Более того, ни один из этих шагов не равен двум полутонам, так как разница полутонов (ми-фа, си-до’) равна 16/15. Коротко говоря, полнейшая галиматья.

Кроме того, натуральный или чистый строй совершенно не решает проблему транспонирования. На самом деле он ее только усугубляет, потому что каждое транспонирование на квинту дает две новые ноты вместо одной. Например, транспонирование гаммы от до до соль дает не только новую ноту фа-диез, но и еще ля, которая отличается от этой же ноты в тональности до. Разница частот является результатом несовпадения между двумя типами шагов в целый тон, 9/8 и 10/9, равняется 1.0125 и называется синтонической коммой.

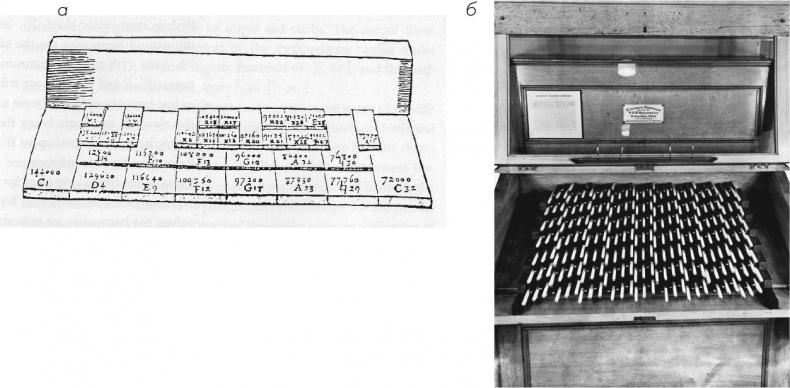
Рис. 3.16 Клавиатура, изобретенная Мареном Мерсенном (а), и фисгармония Роберта Бозанкета (б) были разработаны с целью включить в октаву более двенадцати нот в рамках требований неравномерной темперации.

Примечательно, что теоретики музыки указанного периода решили жить с этой проблемой, хотя для инструментов с фиксированной высотой звука, таких как орган и клавесин, это означало появление дополнительных нот при различной настройке (музыканты, игравшие на струнных инструментах, могли приспособиться, точно определив место прижимания струны, хотя эта задача была серьезным испытанием их точности и ловкости). Клавиатура, которую в 1630-х годах изобрел французский математик Марен Мерсенн, включала тридцать одну ноту в диапазоне октавы, в том числе пятнадцать между фа и ля (Рис. 3.16а). Кажется, что на этом играть просто невозможно, хотя есть информация, что виртуозный Йозеф Гайдн якобы давал на таком инструменте концерты в Нидерландах. Другие системы настройки, которые появились за прошедшие века, предлагали еще более абсурдную градацию нот: фисгармония Бозанкета – инструмент с нетрадиционной настройкой, созданный в 1870-х годах по заказу ученого и теоретика музыки Роберта Холфорда Бозанкета, – имела 84 ноты в октаве (Рис. 3.17б).

Еще одним популярным решением неурядиц пифагорова строя был среднетоновый строй, который появился в начале пятнадцатого века. Он основан на том же методе прибавления нот через цепочку чистых квинт, но справляется с фундаментальной проблемой невозможности абсолютно точно вписать в целое число октавных шагов какого-либо количества шагов в чистую квинту: соотношение частот квинт намеренно уменьшалось относительно «идеальной» пропорции 3:2. Самый распространенный среднетоновый строй на четверть коммы был впервые описан в 1523 году флорентийским теоретиком музыки Пьетро Аароном. Аарон сократил каждую чистую квинту на ¼ синтонической коммы. Четыре шага укороченной квинты приводили к мажорной терции двумя октавами выше. Однако все квинты невозможно последовательно преобразовать таким способом: одна из них оказалась значительно «шире» и получила название волчий интервал (из-за высокого «воющего» звука). Кроме того, в октаве по-прежнему оставалось более двенадцати нот: диезы и бемоли не совпадали.

Решение всех этих проблем в принципе было достаточно ясным. Если октава просто делится на двенадцать равных хроматических шагов, каждый из которых состоит из полутона, то последовательность идентичных по высоте шагов, таких как последовательность мажорного звукоряда тон-тон-полутон-тон-тон-тон-полутон, может начинаться с любой ноты и всегда звучать одинаково. Вопрос заключается в том, каким должен быть это базовый интервал? Не отрекаясь от идеи о каком-либо относительно простом соотношении частот, отец Галилео Галилея, Винченцо, который учился в традиции Царлино, в 1581 году предположил, что повышение полутона должно совпадать с увеличением частоты на фактор 18/17. Двенадцать таких шагов повышают первоначальную частоту примерно на 1.9855, что очень близко к идеальному фактору 2. Но это означало бы, что интервалы в октаву, квинту и кварту лишатся своих идеальных ценных качеств – они окажутся немного снижены, что было бы грубейшим оскорблением классической идеи о гармонии, поэтому предложение не было принято.

Нужно было точное решение проблемы; его открытие произошло практически одновременно в двух разных местах, в Китае и Голландии. Только один фактор, который умножается сам на себя двенадцать раз (по разу на каждый полутон), способен дать точное удвоение частоты, и это корень из двух в двенадцатой степени ¹²√2 или 2^1/12. Такое определение полутона давало более «идеальное» звучание квинт и кварт, чем предложенное Винченцо Галилеем соотношение 18/17: кварта больше тоники на фактор 1.3348 (по сравнению с пифагорейской 4/3 или 1,3333), а квинта на 1,4983 (по сравнению с 3/2 или 1,5).

Эта система называется равномерной темперацией. Впервые она была опубликована в 1584 году китайским ученым Чжу Цзайюем, принцем династии Мин, а фламандский математик Симон Стевин выдвинул ту же идею годом позже. Некоторые утверждают, что Стевин был знаком с концепцией Чжу, что вполне может быть правдой: с 1580 года каждые два года в португальской колонии Макао в дельте Жемчужной реки проходила торговая ярмарка, где европейцы и китайцы обменивались не только товарами, но и идеями; однако прямая связь между Чжу и Стевиным не установлена. В дальнейшем система равномерной темперации была развита в начале семнадцатого века Мерсенном, несмотря на его пристрастие к инструментам с натуральным строем.

Однако у системы равномерной темперации существует философский недостаток, ведь 2^1/12 не только сложное число, но еще и иррациональное, то есть его нельзя представить в виде дроби целых чисел. А как же гармоничная математика пифагорейской концепции музыки? Стевина это не тревожило. Что такого особенного в пифагоровой квинте, спрашивал он, если она ведет к полутону, основанному на жутком соотношении 256/243? С точки зрения математика 2^1/12 – весьма утонченная цифра, и если кто-то думает иначе, это его личные проблемы.

Множество людей с ним не соглашалось, а многие не согласны до сих пор: они настаивают, что система равномерной темперации нанесла ущерб «правильной» гармонии и заставила ее звучать грубо по сравнению с более ранними альтернативными вариантами строя. Герман фон Гельмгольц, немецкий физиолог, который в девятнадцатом веке стоял у истоков понимания акустики, утверждал, что равномерная темперация «неприятна для неиспорченного слуха». В самом деле, разницу между двумя системами нельзя было не заметить: интервал большая терция вызывал самые большие споры. В системе равномерной темперации он был выше почти на один процент, чем в чистом строе, а для большинства людей эта разница прекрасно слышна. Как мы вскоре убедимся, любые споры на тему «превосходства» одной системы настройки над другой лишены основания и в целом сводятся к разговорам о том, кто к чему больше привык. ^[12]