Код. Тайный язык информатики - Чарльз Петцольд Страница 19

Когда в 1973 году Тони Орландо в своей песне попросил, чтобы любимая «повязала желтую ленточку вокруг старого дуба», он не сопроводил свою просьбу ни подробными объяснениями, ни долгими рассуждениями. Никаких «если», «и», «но». Несмотря на сложные чувства и эмоции, сопровождавшие ситуацию, что разворачивалась в реальной жизни и легла в основу песни, мужчине хотелось получить простой ответ: «да» или «нет». Он знал, что, если на старом дубе появится желтая ленточка, это будет означать: «Да, хотя ты и наворотил дел и провел три года в тюрьме, я все равно хочу, чтобы ты вернулся и мы жили под одной крышей». А отсутствие желтой ленточки скажет: «Даже не думай здесь останавливаться».

Здесь есть две четкие взаимоисключающие альтернативы. Тони Орландо не пел: «Повяжи половину желтой ленточки, если тебе нужно время на размышление» или «Повяжи голубую ленточку, если больше не любишь меня, но по-прежнему хочешь остаться друзьями». Нет, он все сформулировал очень просто.

Не менее информативно, нежели отсутствие или наличие желтой ленточки (разве что не столь поэтично), сработал бы дорожный знак, поставленный во дворе, например «Путь открыт» или «Въезд запрещен». Или табличка на двери «Закрыто» или «Открыто». Или фонарик на окне — включенный или выключенный.

Если вам нужно просто сказать «да» или «нет», то способов хватает. Для этого не надо произносить ни одной фразы, слова, даже буквы. Необходим всего один бит, то есть 0 или 1.

Как мы узнали в предыдущих главах, десятеричная система, которой мы пользуемся при подсчете предметов, на самом деле ничем не примечательна. Ясно, что мы пользуемся системой с основанием 10, так как у нас 10 пальцев на руках. Мы могли бы с тем же успехом использовать систему с основанием 8 (будь мы мультяшками), 4 (будь мы омарами) или даже 2 (если бы мы были дельфинами).

Однако двоичная система счисления все-таки особенная. Дело в том, что это простейшая возможная система счисления. В двоичной системе всего две цифры: 0 и 1. Если нам нужно что-то проще двоичной системы, придется избавиться от 1, и останется только 0. Имея всего лишь 0, ничего не сделаешь.

Слово «бит» — сокращение от английского выражения binary digit («двоичная цифра»). Пожалуй, это одно из симпатичнейших слов в компьютерной терминологии. В английском языке у слова bit есть и общеупотребительное значение — «кусочек, небольшая часть», и это значение нам отлично подходит, поскольку один бит — двоичная цифра, мельчайший фрагмент информации.

Иногда, если изобретается новое слово, ему присваивается новое значение. В данном случае все именно так. Слово «бит» — это не только двоичные цифры, при помощи которых удобно считать дельфинам. В компьютерную эпоху это слово приобрело значение «мельчайший первичный фрагмент информации».

Да, смелое утверждение. Естественно, информация передается не только при помощи битов. Буквы, слова, азбука Морзе и шрифт Брайля, а также десятеричные цифры тоже переносят информацию. Суть бита заключается в том, что он передает очень мало информации. Один бит — это минимально возможное количество информации. Меньше бита — отсутствие информации.

Поскольку бит выражает минимальный возможный объем информации, более сложную информацию можно передать некоторым количеством битов. (Говоря, что бит передает мало информации, я совершенно не имею в виду, что эта информация граничит с бессмыслицей. Желтая ленточка очень важна для тех, кто в ней заинтересован.)

«Запомните, дети, — слышал весь мир, // Как в полночь глухую скакал Поль Ревир…» — писал Генри Лонгфелло. Возможно, он исторически недостоверно описал поступок Поля Ревира, предупредившего американских колонистов о вторжении британцев, однако эти стихи замечательно демонстрируют, как можно передать важную информацию при помощи битов.

Он другу сказал: «Я сигнала жду. Коль ночью из города наступать Начнут британцы, ты дай мне знать, На Северной церкви зажги звезду, — Одну, если сушей, а морем — две» ^[13].

Итак, Ревир дал другу два фонаря. Если британцы вторгнутся по суше, друг зажжет на колокольне один, если высадятся с моря — то зажжет оба.

Правда, Лонгфелло не дает явного указания на все случаи жизни. Он умалчивает о третьей возможности, означающей, что британцы пока не вторгаются. Лонгфелло подразумевает, что тогда ни одного фонаря на колокольне гореть не будет.

Допустим, два фонаря висят на колокольне всегда. Как правило, они не горят.

Значит, британцы пока не наступают. Если зажжен один фонарь, значит, британцы наступают по суше, если горят оба, — высаживаются с моря.

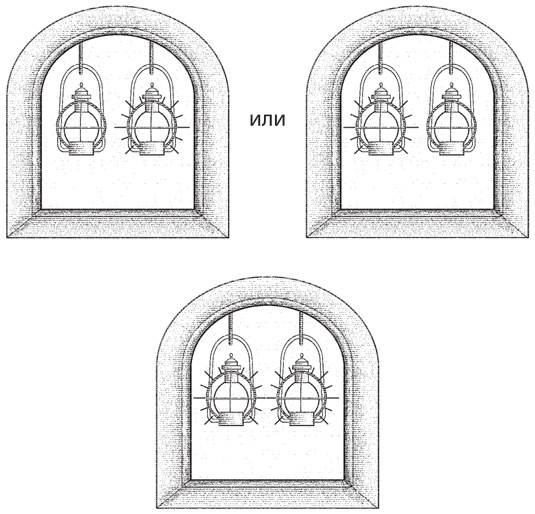
Каждый фонарь — это один бит. Зажженный фонарь равен единичному биту, незажженный — нулевому биту. Тони Орландо показал, что для описания любой из двух возможностей достаточно всего одного бита. Если бы Поль Ревир должен был оповестить людей лишь о том, вторгаются британцы или нет (а не откуда именно), то хватило бы и одного фонаря. Фонарь горел бы в случае нападения и был бы потушен, если бы предстоял еще один спокойный вечер.

Чтобы описать одну из трех возможностей, требуется два фонаря. При наличии второго фонаря и двух битов уже можно описать четыре возможности:

00 = британцы пока не наступают;

01 = британцы наступают с суши;

10 = британцы наступают с суши;

11 = британцы наступают с моря.

На самом деле Поль Ревир, ограничившись всего тремя возможностями, поступил весьма хитроумно. В телекоммуникационной терминологии можно сказать, что он задействовал избыточность, позволяющую бороться с шумом. Термин «шум» в теории телекоммуникаций означает любые помехи, осложняющие передачу информации. Типичный пример шума — помехи на телефонной линии. Тем не менее, даже несмотря на помехи, общение по телефону обычно проходит успешно, поскольку устная речь крайне избыточна. Не требуется четко слышать каждый слог в каждом слове, чтобы понять, что сказали.

В случае с фонарями на колокольне к «шуму» можно отнести такие факторы, как темнота и расстояние от Поля Ревира до колокольни, которые могут помешать отличить первый фонарь от второго. Вот важнейший отрывок из стихов Лонгфелло:

Вдруг видит — звездой огонек замигал,

То дан с колокольни желанный сигнал!

В седло он вскочил, сжал повод в ладонь.