Опасная идея Дарвина: Эволюция и смысл жизни - Дэниел К. Деннетт Страница 18

Поскольку большинство математических обсуждений алгоритмов сосредоточено на их гарантированной или математически доказанной эффективности, люди иногда допускают простейшую ошибку, считая, что процесс, эксплуатирующий случайность или беспорядочность, алгоритмом не является. Но даже при делении в столбик есть место случайности!

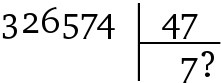
Помещается ли делитель в делимом шесть, семь или восемь раз? Как знать! Да и кому это интересно? Этого и не нужно знать: для того чтобы делить в столбик, большого ума не надо. Алгоритм просто требует, чтобы вы выбрали число – любое, если вам угодно, – и проверили результат. Если избранное число слишком мало, увеличьте его на единицу и начните заново; если оно слишком велико – уменьшите. Относительно деления в столбик можно быть уверенным в одном: оно всегда в конечном счете получается, даже если ваш первоначальный выбор максимально неудачен (в этом случае процесс просто займет немного больше времени). Компьютеры успешно решают сложные задачи несмотря на крайнюю глупость – и именно потому кажутся волшебным изобретением: как что-то настолько безмозглое, как машина, может делать что-то настолько толковое? Итак, не вызывает удивления то, сколь часто интересные алгоритмы используют тактику уточнения выбора, механически проверяя каждого взятого наугад кандидата. Это не только не влияет на их доказуемую эффективность – зачастую именно в этом секрет их эффективности ⁶³.

Для начала можно сосредоточиться на группе эволюционных алгоритмов, рассмотрев повседневные алгоритмы, обладающие теми же важными особенностями. Дарвин привлекает наше внимание к повторяющимся волнам соперничества и отбора, так что возьмем обычный алгоритм организации турнира с выбыванием (например, теннисного), который неизбежно венчается четвертьфиналами, полуфиналами и, наконец, финалом, в ходе которого определяется единственный победитель.

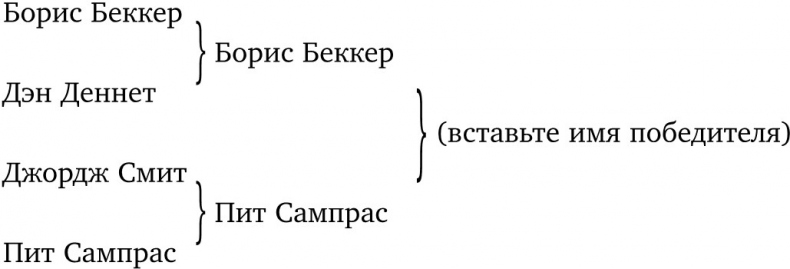
Заметим, что такая процедура удовлетворяет трем условиям. Процедура не изменится, ведем ли мы счет мелом на доске, в компьютерном файле или – необычная возможность – вообще ничего не записываем, а просто осуществляем отбор, веером расположив несколько отгороженных друг от друга теннисных кортов, у каждого из которых две калитки на вход и лишь одна на выход – и через нее победитель попадает на корт, где состоится следующий матч. (А проигравших пристреливают и прикапывают на месте.) Не нужно быть гением, чтобы провести участников состязания через такое «сито», в конце каждого матча заполняя бумаги (или расстреливая проигравших). Алгоритм всегда сработает.

Но что именно он делает? На входе мы имеем некоторое количество участников и гарантию уничтожения для всех, кроме единственного победителя. Но что представляет собой победитель? Это зависит от состязания. Допустим, мы устраиваем не теннисный турнир, а состязание по бросанию монеты. Один из игроков подбрасывает монетку, другой выбирает орла или решку; победитель продвигается на шаг вперед. Победителем такого состязания станет один-единственный игрок, который n раз последовательно победит при подбрасывании монеты, ни разу не проиграв – в зависимости от того, сколько раундов потребуется для завершения состязания.

В таком состязании есть нечто странное и глупое – но что? Победитель и в самом деле обладает весьма примечательным качеством. Часто ли вы встречаете людей, которые, подбрасывая монетку, без единого проигрыша выиграли десять раз подряд? Скорее всего, ни разу. Шансы на появление такого человека могут показаться ничтожными, и при обычном стечении обстоятельств это так и есть. Если какой-нибудь аферист предложит вам побиться об заклад десять к одному, что он сможет привести человека, который у вас на глазах десять раз подряд выиграет в состязании по бросанию монеты (и монета не будет фальшивой), вы, вероятно, склонны будете счесть это пари выигрышным для себя. Если так, будем надеяться, что у этого афериста не нашлось 1024 сообщников (им не придется жульничать – они будут играть абсолютно честно): ведь именно столько (2¹⁰ участников состязания) нужно, чтобы организовать десятираундный турнир. В начале турнира аферист никак не сможет предсказать, кто именно окажется «вещественным доказательством А», которое обеспечит ему выигрыш пари, но алгоритм проведения турнира неизбежно – и быстро – выявит этого человека: так что вас обманули, и аферист непременно выиграет. (Я не несу ответственности за ущерб, который вы можете понести, попытавшись воспользоваться этим изысканным образчиком практической философии в корыстных целях.)

В любом турнире с выбыванием бывает победитель, который «автоматически» обладает качеством, необходимым, чтобы пройти все этапы состязания, но, как показывает соревнование в бросании монеты, такое качество может быть «всего лишь историческим» – банальным фактом биографии участника состязания, никак не влияющим на его или ее виды на будущее. Представим, например, что ООН принимает постановление впредь разрешать все международные конфликты, подбрасывая монетку, – участвовать в таком соревновании должны представители конфликтующих сторон (если в конфликт вовлечено более одного народа, придется организовывать какой-то турнир: можно использовать круговую систему – алгоритм тогда будет другим). Кого следует выбрать представителем нашей нации? Естественно, того, кто лучше всех бросает монетку. Допустим, мы организовали масштабный турнир с выбыванием, в котором принимают участие все мужчины, женщины и дети США. Кто-то в нем победит – этот человек последовательно выиграет в двадцати восьми раундах без единого проигрыша. Победа будет неопровержимым фактом его биографии, но, поскольку подбрасывание монеты – дело случая, нет никаких оснований полагать, что победитель такого турнира покажет себя на международных соревнованиях лучше, чем кто-либо, проигравший в одном из предыдущих раундов. У случая нет памяти. Человек, у которого в руках выигрышный лотерейный билет, безусловно, был удачлив, и благодаря только что выигранным миллионам удача ему может больше никогда не понадобиться; тем лучше, ведь нет оснований считать, что его шансы во второй раз выиграть в лотерею выше, чем у любого другого участника – или что, скажи он «орел», монета упадет загаданной стороной вверх. (Неспособность принять тот факт, что у случая нет памяти, известна как ошибка игрока; это заблуждение удивительно широко распространено – настолько широко, что мне, вероятно, следует подчеркнуть, что это – без всяких сомнений и оговорок – заблуждение.)

В противоположность соревнованиям, где правит случай (например, соревнованиям в бросании монеты), существуют соревнования, где все решает мастерство – например, теннисные турниры. Здесь есть основания полагать, что игроки, вышедшие в последние раунды, снова преуспеют, если выставить их против тех, кто вылетел из состязания раньше. Есть основания – но никаких гарантий – полагать, что победитель такого турнира – самый лучший игрок и будет лучшим не только сегодня, но и завтра. Тем не менее, хотя любой разумно организованный турнир неизбежно позволит назвать победителя, нет гарантий, что в ходе состязания в мастерстве победитель окажется лучшим игроком во всех (значимых) смыслах этого слова. Вот почему на церемонии открытия мы иногда говорим: «Пусть победит сильнейший!» – процедура не гарантирует подобный исход. Лучший игрок – тот, кто является лучшим по «техническим» критериям (обладатель самого мощного удара левой, самой быстрой подачи, самой высокой выносливости и т. д.), – может встать не с той ноги, вывихнуть лодыжку – или его может ударить молния. Тогда, очевидно, в состязании его обойдет игрок похуже. Но никто не станет организовывать или участвовать в соревнованиях в мастерстве, если бы в конце концов их не выигрывали лучшие игроки. Это гарантирует само определение честного состязания в мастерстве; если бы лучшие игроки выигрывали в каждом раунде с вероятностью не выше 50%, речь шла бы о состязании в удачливости, а не в мастерстве.