Музыкальный инстинкт. Почему мы любим музыку - Филип Болл Страница 17

В любом случае к тому времени, как Птолемей (знаток музыки и астрономии) написал свой трактат «Гармоника» («Harmonia») во втором веке н. э., существовало семь ладов и они, видимо, приобрели статус гамм или звукорядов (Рис. 3.11). Самым распространенным был дорийский, который соответствует западной минорной гамме. Фригийский лад Птолемея тоже был «минорным», а лидийский является эквивалентом мажорной гаммы. Эти лады с некоторыми модификациями перешли в средневековую западную культуру, где их записывали нотами для литургических песнопений. К сожалению, отчасти из-за неправильной средневековой интерпретации, лады литургической музыки того времени располагают на других нотах, чем у их древнегреческих тезок (Рис. 3.12). Греческий миксолидийский лад, например, проходит от си до си’ по белым клавишам, а средневековый миксолидийский – это гамма из белых клавиш от соль до соль’. Позже теоретики музыки представили новые лады, которым они дали античные имена: ионийский, разработанный швейцарцем Генрихом Глареаном в шестнадцатом веке, больше всего напоминает мажорную гамму, и эолийский, который в наши дни является одной из минорных гамм.

В диатонических звукорядах, которые используются сегодня, каждая гамма основана на определенной ноте (тонике). Средневековые лады не обладали тоникой, но в них присутствовали аналогичные закрепленные ноты. Одна из них называлась «финалис»: в так называемых натуральных ладах серия нот начиналась (здесь легко запутаться) с финалиса, а в плагальных ладах после финалиса начинается чистая кварта (Рис. 3.12). В большинстве псалмов в основе лежат простые формульные мелодии, называемые псалмовым тоном, где большая часть текста пропевается на одном «распевном тоне» под названием «тенор» (от латинского слова «tenere» – удерживать). Кроме того, существовали специальные псалмовые тоны, связанные с отдельными ладами. Получается, что не у всех нот в ладу был равный статус: финалис и тенор были особенными, подобно тому как некоторые ноты (например, тоника, терция и квинта) пользуются особыми привилегиями в диатонической тональной музыке.

Чтобы средневековым монахам было легче запоминать ноты, итальянский священнослужитель одиннадцатого века Гвидо д’Ареццо придумал удобное мнемоническое правило: ноты до, ре, ми, фа, соль, ля, заметил он, последовательно начинают строфы общеизвестного гимна «Ut queant laxis» слогами ut-re-mi-fa-sol-la. Добавив седьмую ноту ti и заменив ut на do, из грегорианского псалма мы перенесемся сразу к Джули Эндрюс и хору австрийских детей, распевающих мажорную гамму.

Последовательность д’Ареццо из шести нот, имеющая название гексахорд, состоит из нот, разделенных целым тоном, кроме двух средних (ми, фа), которые отстоят друг от друга на полутон. Он предложил музыкальную схему, в которой все используемые ноты образуют серию гексахордов, начиная с соль, до и фа. Мелодии средневековых псалмов обладали высотой тона в диапазоне почти трех октав, от низкой соль до высокой ми. Самая низкая соль обозначалась греческим символом гамма как первая нота гексахорда и называлась gamma ut. К этому названию восходит английское слово «gamut» – гамма.

Чтобы сохранить шаг высоты тона в гексахорде, если серия начинается с фа, оду из «белых нот» приходится заменять. Так гексахорд состоит из фа, соль, ля, си, до, ре. Чтобы третий шаг остался полутоном, а четвертый целым тоном, си нужно уменьшить до полутона: говоря современным языком, ноту нужно понизить до си-бемоль. Таким образом появились новые символы для обозначения си-бемоль в гексахорде фа и «натуральной» си в гексахорде соль (гексахорд до не доходит до си). Первая обозначалась круглой буквой «b», или «мягкой b» (B molle), а вторая квадратной буквой «b», или «твердой b» (B durum). Отсюда пошли современные символы низкого варианта ноты и бекара (♭ и). Символ высокого варианта ноты ♯ также соотносится с последним. Таким образом, средневековая система гексахорда послужила истоком первого знака альтерации – модификации нот с целью попасть в нужную «гамму». С высоты современной тональной структуры мы можем сказать, что гексахорд с фа – это транспозиция гексахорда с до или соль в новую тональность.

Смена тональности

Каким бы «естественным» ни казался пифагоров строй, он страдает от серьезного недостатка, даже от двух связанных между собой недостатков. Во-первых, мы начали с тезиса, что все гармонические звуки происходят из комбинации тонов с простым соотношением частот, но каким-то образом пришли к звукоряду, в котором содержатся соотношения высоты тона вроде 81/64 и 243/128, а это не кажется таким уж простым! Во-вторых, «большой» шаг пифагорова строя соответствует целому тону, а малые шаги – полутону. Значит, два малых шага должны в совокупности представлять то же, что и один большой шаг; но так не происходит! Повышение высоты на два полутона означает умножение частоты на (256/243)²!

И рождается пугающая дробь, которая не равна соотношению целого тона 9/8. Вообще, эти значения довольно близки, так что, может, нам не нужно беспокоиться? Но нет, беспокоиться нужно. Из-за этого несоответствия пифагорова система не может дать нам небольшой набор нот, из которых мы можем сочинять музыку, – вместо этого она дает бесконечное число нот.

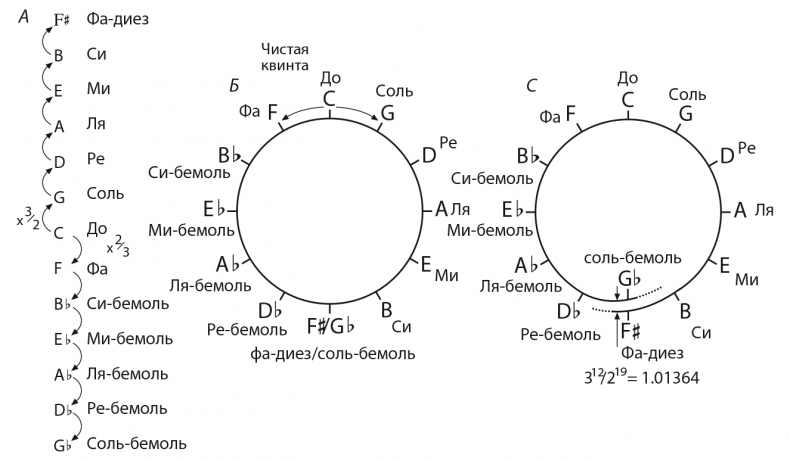
Рис. 3.13 Все хроматические ноты в западной гамме можно найти через повторяющийся цикл квинт (а). В конечном счете восходящий цикл приводит нас к фа-диез, а нисходящий цикл – к соль-бемоль. На современном фортепиано эти ноты эквивалентны – они находятся на одной и той же клавише, что означает, что цепочка квинт замкнулась (б). Но в пифагорейской системе, где каждый шаг строго соответствует «математической» чистой квинте (с соотношением частот 3/2), фа-диез и соль-бемоль не совпадают: их частоты отличаются на фактор, известный как пифагорейская комма, равная примерно 1.01364. То есть цепочка не замыкается, а движется по спирали (с). Независимо от длины цепочки квинт, мы никогда не дойдем до точки соприкосновения и будем все время получать новые ноты.

Как это произошло? Мы увидели, что одним из способов конструирования пифагорейской гаммы служит последовательное движение вверх изначальной ноты (тоники) на чистую квинту. Исключение составляет четвертая нота гаммы, фа в тональности до, которую мы отыскиваем шагом вниз на чистую квинту от тоники (соотношение частот).

Если мы продолжим этот цикл квинт, то обнаружим ноты не мажорной гаммы, а хроматической. Квинта вверх от си приведет нас к фа-диез, квинта вниз от фа – к си-бемоль (соотношение частот 2⁴/3²:1 или 16/9), а затем последовательно к ми-бемоль, ля-бемоль, ре-бемоль и соль-бемоль (Рис. 3.13а).

Кризис налицо. На фортепианной клавиатуре фа-диез и соль-бемоль являются эквивалентными нотами: они обе играются одной и той же клавишей. Другими словами, фа-диез и соль-бемоль представляют собой точку, где так называемый цикл квинт, начатый с до, замыкается сам на себе в полный круг (Рис. 3.13б). Но в пифагоровом строе ноты фа-диез и соль-бемоль не одинаковы: фа-диез, к которой мы приходим восходящими шагами, обладает частотой 3⁶/2⁹ или 729/512 раз от до. А частота соль-бемоль, которую мы находим, двигаясь вниз, превосходит до на фактор 2¹⁰/3⁶ или 1024/729. Разница совсем небольшая: примерно 1.01364 или, если совершенно точно, соотношение 3¹²/2¹⁹; оно известно как пифагорейская комма.