Укрощение бесконечности. История математики от первых чисел до теории хаоса - Йен Стюарт Страница 16
Укрощение бесконечности. История математики от первых чисел до теории хаоса - Йен Стюарт читать онлайн бесплатно
Ознакомительный фрагмент
Как развивалась алгебра? Сначала это были задачи и методы. Со временем она приобрела символическую систему обозначений, которую мы считаем ее главным достоинством. Было много систем обозначений, но постепенно одна вытеснила конкурентов. Само название «алгебра» тоже возникло в процессе, и оно имеет арабские корни (об этом говорит начальное «аль», арабский эквивалент артикля the, что и указывает на происхождение).
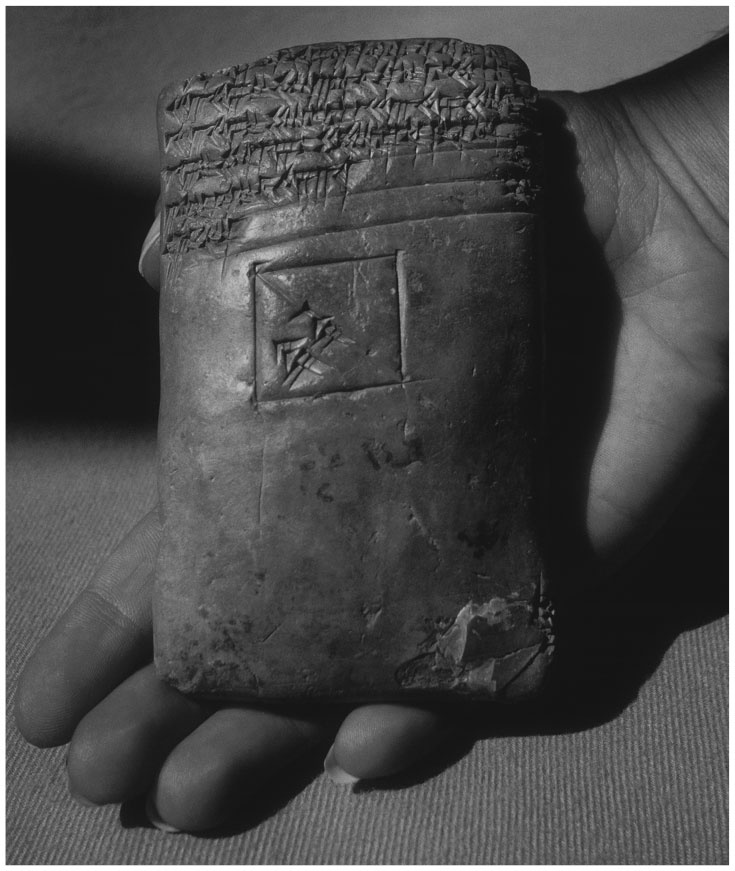
Табличка из Старого Вавилона с клинописной записью алгебро-геометрической задачи
То, что мы сейчас называем решением уравнений (когда неизвестная величина должна быть найдена на основе имеющейся информации), почти так же старо, как и арифметика. Есть косвенные доказательства тому, что вавилоняне умели решать весьма сложные уравнения еще в 2000 г. до н. э., и прямые свидетельства решения несложных задач в виде клинописных табличек, датируемых примерно 1700 г. до н. э.
Сохранившаяся часть таблички YBC 4652, из периода Старого Вавилона, содержит 11 простых задач для решения, а по сопроводительному тексту можно понять, что изначально их было двадцать две. Вот типичный вопрос:
«Я нашел камень, но не знаю его вес. После того как я взял его вес шесть раз, добавил 2 джина и добавил одну треть от одной седьмой [этого нового веса], умноженной на 24, я взвесил его. В результате получилось 1 ма-на. Сколько весил исходный камень?»
Вес 1 ма-на равен 60 джинов.
В современных обозначениях мы примем за x вес исходного камня в джинах. Тогда решение будет выглядеть так:
(6x + 2) + 1/3 × 1/7 × 24(6x + 2) = 60,
и стандартные алгебраические методы дают результат 4 1/3 джина. На табличке есть этот ответ, но нет решения, объясняющего, как он был получен.
Явно его получили не с использованием символических методов, похожих на современные, поскольку ниже в табличке прописаны методы решения с точки зрения типичных учебных примеров: «Поделите пополам это число, добавьте сумму этих двух, извлеките квадратный корень…» и т. д.
Эта задача, заодно с прочими на табличке YBC 4652, представляет то, что сейчас мы зовем линейными уравнениями: неизвестное x входит в него только в первой степени. Любое из линейных уравнений можно представить в виде
ax + b = 0,
с решением x = –b/a. Но в древние времена, когда не было понятий отрицательных чисел и символьных операций, поиск результата был не так прост. Даже сейчас некоторые школьники не сразу решат задачи с таблички YBC 4652.
Интереснее квадратные уравнения, в которых неизвестное возведено во вторую степень – квадрат. В современной формулировке это уравнение вида:
ax2 + bx + c = 0,
и здесь тоже есть стандартная формула для вычисления x. Подход древних вавилонян к этим уравнениям изложен в задаче на табличке BM 13901:
«Я семь раз добавил сторону моего квадрата и 11 раз – его площадь, [получив] 6;15».
Здесь 6;15 – упрощенная форма вавилонской шестидесятиричной системы и означает 6 плюс 15/60, или 6 1/4 в современных обозначениях. Предлагаемое решение начинается так:
«Запиши 7 и 11. Умножь 6;15 на 11, [получи] 1,8;45. Раздели 7 на 2, [получи] 3;30 и 3;30. Перемножь, [и получи] 12;15. Сложи [это] с 1,8;45, [получи] результат 1,21. Это есть квадрат 9. Вычти 3;30, которое ты перемножал, из 9. Результат вычисления 5;30. Величину, обратную к 11, нельзя найти. На что надо умножить 11, чтобы получить 5;30? [Ответ равен] 0;30, сторона квадрата равна 0;30».
Обратите внимание: табличка указывает читателю, что делать, но не почему. Это не более чем алгоритм. Кому-то необходимо было понять, как это работает, прежде всего чтобы записать способ решения. Но, будучи однажды открытым, он становится доступным каждому обученному. Мы так и не знаем, то ли вавилоняне заучивали алгоритм наизусть, то ли должны были сами объяснять, почему он работает.
Приведенный выше алгоритм выглядит размытым, однако интерпретировать его всё же проще, чем мы могли бы подумать. И здесь очень помогает использование рациональных чисел: мы сразу понимаем, какие правила пошли в ход. Чтобы обнаружить их, достаточно просто привести всё к системе. В современной записи имеем:
a = 11, b = 7, c = 6;15 = 61/4.
Тогда уравнение примет вид:
ax2 + bx = c,
соответственно с данными значениями для a, b и c. Нам нужно найти x. Вавилонское решение диктует нам следующее.
1. Умножить с на а, чтобы получить ас.
2. Разделить b на 2, чтобы получить b/2.
3. Возвести в квадрат b/2, чтобы получить b2/4.
4. Сложить это с ас, что даст ас + b2/4.
5. Извлечь из этого квадратный корень, чтобы получить
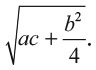
6. Вычесть из этого b/2, чтобы получить
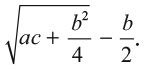
7. Разделить это на а, и ответ будет
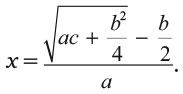
Это эквивалентно формуле
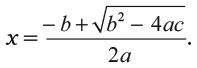
Вавилоняне явно отдавали себе отчет в том, что их решения являются неким обобщением. Приведенный пример слишком сложен, и его можно считать специальным, подобранным только для данной задачи.
Как относились к своему методу сами вавилоняне и что о нем думали? Похоже, должна была быть некая упрощенная идея, лежавшая в основе такого сложного процесса. Возможно, хотя напрямую это и не доказано, что они изобрели некую геометрическую идею, дополняющую квадрат. Алгебраическая версия этого метода также рассматривается в наши дни. Для ответа на этот вопрос мы его для ясности запишем в виде x2 + ax = b и приведем на рисунке его геометрическую интерпретацию.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии