Пространство - это вопрос времени. Эйнштейн. Теория относительности - Давид Бланко Ласерна Страница 15

А’ и В’ считают, что находятся в состоянии покоя. А’ засекает на своем хронометре время выстрела мяча (t’1) (рисунок 11). Когда мяч ударяется о стену, В’ отмечает момент времени на своем секундомере (t'₂) (рисунок 12).

Зная скорость v и время t' и t'₁ в системе отсчета D можно сделать вывод о расстоянии, пройденном мячом, умножив скорость на период времени. В этом случае:

L'=v•(t'₂ -t'₁).

Версия наблюдателей на причале

Нам снова понадобится целый ряд наблюдателей, стоящих вдоль причала, – каждый с хронометром. Пусть А – наблюдатель, который находится напротив метательной машины в момент выстрела. Он отметит на своем хронометре момент вылета мяча из машины (t₁) (рисунок 13). В – тот, кто будет находиться напротив мяча, когда тот ударится о стену. В момент удара он отметит время t₂ (рисунок 14).

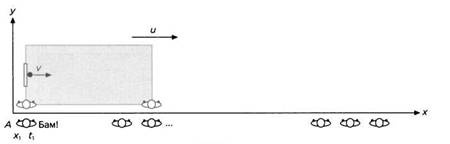
РИС. 13

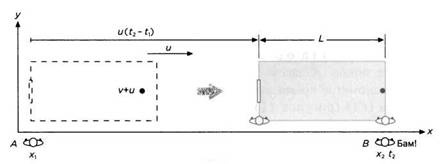
РИС. 14

Наблюдатели считают, что скорость мяча внутри метательной машины уже равна скорости движения корабля и. После выстрела правая стена смещается, отдаляясь от мяча со скоростью u потому мяч должен пройти большую дистанцию. Поэтому несмотря на то, что наблюдатели системы G отметят то же время, что и наблюдатели системы D пройденное расстояние и скорость мяча для них будут разными:

L+u•(t₂-t₁) где u•(t₂-t₁) расстояние, на которое отодвигается правая стена в то время, пока мяч находится в воздухе.

Если мы отвлечемся от существования корабля и будем заниматься только мячом, то увидим, что со скоростью v + u он за период времени t₂ – t₁ пролетит расстояние

(v + u)•(t₂- t₁).

Обе величины должны быть равны между собой:

L + u • (t₂ – t₁) = (v + u) • (t₂ – t₁).

Получим знакомое уравнение для вычисления длины трюма:

L = v•(t₂- t₁).

Можно сделать вывод о том, что с точки зрения наблюдателей на причале мяч должен пройти большее расстояние, поскольку стена от него отдаляется, но при этом он летит с большей скоростью, так как к его скорости прибавляется скорость корабля, поэтому оба эффекта компенсируют друг друга.

Электромагнитный эксперимент

Заменим метательную машину фонарем, а мяч – лучом света (и опять мы имеем дело с электромагнитным излучением).

Единственный элемент, общий для систем G и D – величина скорости света. Все хронометры, участвующие в эксперименте, произведены на одной фабрике, но только два из них в одной и той же системе отсчета показывают одно и то же время. Для того чтобы перевести пространственные или временные координаты из одной системы в другую, необходимо прибегнуть к преобразованиям Лоренца.

Версия наблюдателей находящихся в трюме корабля

Как и в механическом эксперименте, А’ отмечает тот момент, когда световой луч выходит из фонаря, а В’ – момент, когда луч достигает противоположной стены (рисунок 15). Для них:

L’ = c-(t'₂ -t'₁).

Версия наблюдателей на причале

С причала наблюдатели видят, как отдаляется правая стена, световой луч при этом по-прежнему движется со скоростью с (рисунок 16). Они замечают, что прежде чем достичь стены, луч преодолел не только длину трюма, но и дистанцию, пройденную кораблем в период времени между t₁ и t₂ (рисунок 17):

L +u-(t₂ -t₁).

С другой стороны, если оставить корабль в стороне, за временной интервал (t₂ – t₁) свет проходит расстояние:

c•(t₂ -t₁)=x2 -x1

Приравняв выражения друг к другу:

L + u • (t₂- t₁) = с • (t₂- t₁)=х2- х1

и применив формулу преобразований Лоренца, мы получаем поразительный результат:

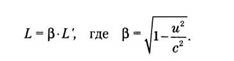
Поскольку скорость корабля меньше скорости света (u < с), то фактор бета меньше t, а значение L меньше, чем L'. То есть для наблюдателей в системе G трюм корабля в длину меньше, чем для наблюдателей в системе D. Это и есть так называемое Лоренцево сжатие.

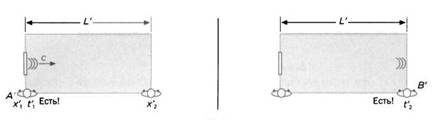
РИС. 15

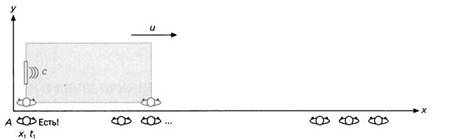
РИС. 16

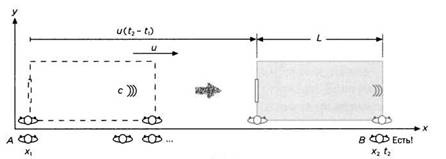
РИС. 17

Математическое выражение сжатия Лоренца

Ниже мы показываем, как преобразования Лоренца применяются в расчете сжатия. У нас есть два математических выражения того расстояния, которое проходит свет:

L + u•(t₂ -t₁),

с•(t₂- t₁)=x2 -х1.

Приравняем их:

L + u•(t₂ -t₁ ) = c•(t₂ -t₁ )=x2- x1 L=x2 -x1 -u-(t₂ -t₁ ).

Уравнение можно упростить, если немного изменить обозначения:

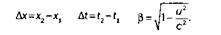
Тогда выражение, найденное для L, сокращается до:

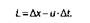
Поскольку теперь мы допускаем, что часы могут идти по-разному в зависимости от системы, для перевода координат системы G в систему D нам будет нужно использовать преобразования Лоренца: