Путеводитель для влюблённых в математику - Эдвард Шейнерман Страница 14
Путеводитель для влюблённых в математику - Эдвард Шейнерман читать онлайн бесплатно
Ознакомительный фрагмент
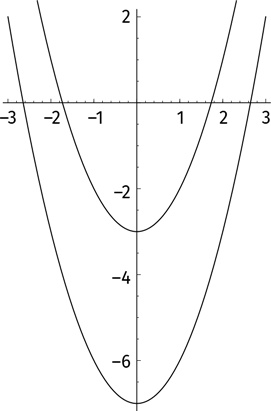
Вопрос кардинально меняется, когда мы ищем такое число, что x² = –1. А существует ли оно в принципе? Если возвести в квадрат положительное число, ответом будет положительное число, скажем 5² = 5 × 5 = 25 > 0. Если возвести в квадрат отрицательное число, результат снова будет положительным числом: (–5)² = (–5) × (–5) = 25 > 0. Если возвести в квадрат ноль, получится ноль. Наше положение выглядит безнадежно.
Мы испытаем еще большее отчаянье, когда нарисуем график уравнения y = x² + 1 и увидим, что парабола нигде не пересекает ось абсцисс.
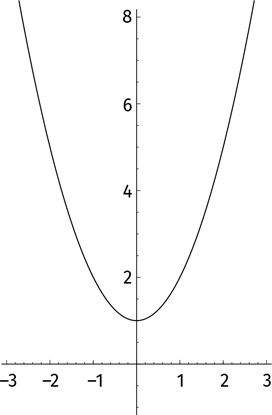
Есть искушение сдаться и объявить: «Нельзя извлекать квадратные корни из отрицательных чисел». На самом деле нам просто не хватает воображения. Да, не существует ни одного действительного числа, удовлетворяющего условию x² = –1, но, возможно, есть какие-то другие?
Мнимые числа
Решение на редкость просто. Раз нет такого действительного числа, что x² = –1, то мы просто создадим новое число, назовем его i и поставим условие i² = –1.
Конечно, в голове сразу зазвучит сигнал тревоги: «Откуда взялось это число? Выдумывать числа нельзя! Что за чепуха!»
Чтобы облегчить душу, назовем новое число мнимым[56]. В наших глазах такое число – второго сорта: мы не кладем i кубиков сахара в чашку кофе и не боимся, что расстояние до университета окажется равным i миль[57].
Мы просто решили поиграть и сами придумали правила. Хорошо, теперь давайте поразмышляем. Посмотрим, на что годно это число i. Мы знаем, что i × i = –1. А как насчет i + i? Если следовать привычным арифметическим правилам, то получится другое мнимое число: 2i. А что, если возвести это число в квадрат? Попробуем!
(2i) ² = (2i) × (2i) = 2 × i × 2 × i = 2 × 2 × i × i = 4 × (i × i) = 4 × (–1) = –4.
Другими словами, число 2i представляет собой квадратный корень из числа –4.
Теперь возведем в квадрат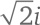 и посмотрим, что получится:
и посмотрим, что получится:
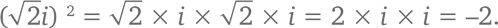
Таким образом,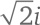 представляет собой квадратный корень из числа –2. Когда мы приютили мнимое число i в семье всех чисел, мы заполучили не просто
представляет собой квадратный корень из числа –2. Когда мы приютили мнимое число i в семье всех чисел, мы заполучили не просто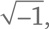 а в придачу еще и квадратные корни из всех отрицательных действительных чисел! Любое число вида b × i, где b – это действительное число, называют мнимым числом.
а в придачу еще и квадратные корни из всех отрицательных действительных чисел! Любое число вида b × i, где b – это действительное число, называют мнимым числом.
Если сложить два мнимых числа, например 2i и 4i, мы получим другое мнимое число: 6i. Если мы перемножим два мнимых числа, например 3i и –2i, то получим действительное число:
3i × (–2i) = 3 × (–2) × i × i = (–6) × (–1) = 6.
Комплексные числа
Чтобы мнимые числа прижились в семье всех чисел, нужно научиться складывать, вычитать, умножать и делить мнимые и действительные числа вместе. Мы будем работать с множеством комплексных чисел. Это расширение множества действительных чисел, включающее все числа вида a + bi, где a и b – действительные числа, например 3 + 4i.
Само число i комплексное, потому что может быть представлено в виде 0 + 1i. Точно так же действительные числа могут быть представлены в виде –7 + 0i.
Складывать комплексные числа несложно, мы просто приводим подобные слагаемые:
(3 + 2i) + (4 – 3i) = (3 + 4) + (2 – 3) i = 7 – i.
Более педантично мы можем записать это так: 7 + (–1) i.
Вычитание ничуть не сложнее:
(3 + 2i) – (4 – 3i) = (3 – 4) + (2 – (–3)) i = –1 + 5i.
Очевидно, что сумма или разность двух комплексных чисел – тоже комплексное число. На языке алгебры мы можем продублировать эту фразу так (числа a, b, c, d здесь – действительные):
(a + bi) + (c + di) = (a + c) + (b + d) i;
(a + bi) – (c + di) = (a – c) + (b – d) i.
Умножение комплексных чисел дается несколько труднее. Попробуем перемножить наших друзей 3 + 2i и 4 – 3i:
(3 + 2i) × (4 – 3i) = 3 × (4 – 3i) + 2i × (4 – 3i) = (3 × 4 – 3 × 3i) + (2i × 4 – 2i × 3i) = (12 – 9i) + (8i + 6) = 18 – i.
На алгебраическом языке произведение двух комплексных чисел выражает формула:
(a + bi) × (c + di) = (ac – bd) + (ad + bc) i.
Очевидно, что при перемножении двух комплексных чисел мы получаем комплексное число.
Из всех арифметических операций деление комплексных чисел сложнее всего. Оно приводит нас к выражению (a + bi) / (c + di), поэтому сначала нам придется поговорить о взаимно обратных числах. Число x называют взаимно обратным числу y, если xy = 1. Например, дробь 1/2 взаимно обратна числу 2.
Конец ознакомительного фрагмента
Купить полную версию книгиЖалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии