Код. Тайный язык информатики - Чарльз Петцольд Страница 14

Наконец человек, чья работа заключалась в рисовании уток, подумал: «Зачем рисовать четырех уток? Не изобразить ли одну и обозначить, что на самом деле уток четыре, скажем, черточками?»

Когда потребовалось нарисовать 27 уток, черточки выглядели нелепо.

Подумалось: «Должен быть другой способ, лучше», — так появилась система чисел.

Из всех древнейших числовых систем до сих пор в ходу римские цифры. Они встречаются на циферблатах, ими выбивают даты на памятниках, нумеруют некоторые страницы в книгах, используют при подсчете некоторых элементов и — что наиболее раздражает — при указании информации об авторских правах в кинофильмах. (Иногда чтобы ответить на вопрос, в каком году был снят фильм, нужно молниеносно расшифровать какие-нибудь MCMLIII в хвосте титров.)

Двадцать семь уток римскими цифрами будет так.

Принцип довольно прост: X означает 10 черточек, V — пять.

Вот римские цифры, сохранившиеся до наших дней.

I V X L C D M

I — это единица; она похожа на черточку или один поднятый палец. V — это пятерка; возможно, этим символом обозначалась ладонь. Из двух V составляется X, то есть десятка.

L — это пятьдесят, C — буква, с которой начинается латинское centum, — сто, D — пять сотен, M — первая буква в слове mille — тысяча.

Хотя мы, возможно, с этим не согласимся, но на протяжении веков считалось, что римские цифры удобны для сложения и вычитания, именно поэтому они так долго использовались в Европе при ведении бухгалтерии. Действительно, при сложении двух римских чисел просто выписываются рядом все символы из двух этих чисел, а затем применяется всего несколько правил: пять I образуют V, две V — X, пять X — L и т. д.

Сложно умножать и делить числа, записанные римскими цифрами. Многие другие ранние числовые системы (например, греческая) аналогично не подходят для сложных математических действий. Древние греки разработали превосходную геометрию, которая до сих пор практически без изменений преподается в школах, но так ли известна древнегреческая алгебра?

Цифры, которыми мы пользуемся сегодня, называются индо-арабскими. Они возникли в Индии, но были занесены в Европу арабскими математиками. Особенно прославился персидский математик Мухаммад ибн Муса аль-Хорезми (от имени которого происходит слово «алгоритм»), написавший около 825 года книгу по алгебре, где пользовался индийскими цифрами. Эта книга была переведена на латынь около 1120 года, оказала большое влияние на Европу и стимулировала переход с римских цифр на современные.

Индо-арабская система чисел отличалась от более ранних.

Индо-арабская система называется позиционной, то есть любая цифра может обозначать в ней разное количество в зависимости от того, в какой части числа стоит. Положение цифры в числе не менее (и даже более) важно, чем значение самой цифры. И в 100, и в 1 000 000 всего по одной единице, но всем известно, что миллион гораздо больше сотни.

Практически во всех ранних системах счисления было нечто, чего нет в индо-арабской системе, а именно: отдельный символ для обозначения десятки. В нашей системе счисления такой символ отсутствует.

С другой стороны, практически во всех ранних числовых системах отсутствовало кое-что, имеющееся в индо-арабской системе и, по сути, более важное, чем символ десятки, — символ нуля.

Да, ноль. Скромный ноль, несомненно, одно из важнейших изобретений в истории чисел и математики. Он обеспечивает позиционную запись, поскольку позволяет отличить 25 от 205 и от 250. Ноль упрощает многие математические действия, неудобные в непозиционных системах, особенно умножение и деление.

Вся структура индо-арабских чисел проясняется, если обратить внимание, как мы их произносим. Например, 4825: «Четыре тысячи восемьсот двадцать пять». Это означает:

четыре тысячи,

восемь сотен,

два десятка

и еще пять.

Либо можно разложить это число на компоненты, например:

4825 = 4000 + 800 + 20 + 5.

Или еще мельче, вот так:

4825 = 4 × 1000 +

8 × 100 +

2 × 10 +

5 × 1.

Или, воспользовавшись степенями десятки, записать следующее:

4825 = 4 × 103 +

8 × 102 +

2 × 101 +

5 × 100.

Напоминаю: любое число в степени 0 равно единице.

Каждая позиция в многозначном числе имеет определенное значение, как показано на следующей схеме. В семи окошках можно записать любое число от 0 до 9 999 999.

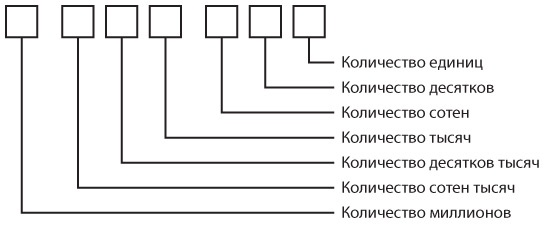
Каждая позиция соответствует степени десятки. Специального символа для десятки не требуется, поскольку 1 просто ставится в нужную позицию, а 0 используется в качестве символа-заполнителя.

Самое замечательное в данном случае в том, что дробные величины, обозначаемые цифрами после десятичной запятой, подчиняются той же закономерности. Число 42 705,684 равно:

4 × 10 000 +

2 × 1000 +

7 × 100 +

0 × 10 +

5 × 1 +

6 ÷ 10 +

8 ÷ 100 +

4 ÷ 1000.

Это число можно записать и без деления:

4 × 10 000 +

2 × 1000 +

7 × 100 +

0 × 10 +

5 × 1 +

6 × 0,1 +

8 × 0,01 +

4 × 0,001.

Или при помощи степеней десятки:

4 × 104 +

2 × 103 +

7 × 102 +

0 × 101 +

5 × 100 +

6 × 10–1 +

8 × 10–2 +