Укрощение бесконечности. История математики от первых чисел до теории хаоса - Йен Стюарт Страница 12
Укрощение бесконечности. История математики от первых чисел до теории хаоса - Йен Стюарт читать онлайн бесплатно
Ознакомительный фрагмент
Чтобы отличать буквы, обозначающие цифры, греки ставили над ними горизонтальную черту. Для чисел больше 999 значение их символа могло быть умножено на 1000, если перед ним поставить штрих.
Разные способы, предложенные греками, удовлетворяли потребность записывать результаты подсчетов, но не были приспособлены для выполнения самих расчетов (попробуйте, например, представить себе умножение σμγ на ωλδ). Возможно, процесс подсчета был заменен использованием абака или просто камешками в песке, особенно в ранние времена.
Дроби греки записывали несколькими путями. Первый – числитель, за ним один штрих (′), а за ним знаменатель с двумя штрихами (′′). Часто знаменатель записывали дважды. Итак, 21/47 будет выглядеть как:
κα′ μζ′′ μζ′,
где κα равно 21, а μζ – 47. Также они использовали дроби, похожие на египетские, где имелся особый символ для 1/2. Некоторые греческие астрономы, особенно Птолемей, использовали шестидесятиричную вавилонскую систему для точности, но греческие символы для самой записи чисел. Это вовсе не похоже на то, чем мы пользуемся сегодня. Фактически это полный хаос.
Символы, которые используются сейчас в десятеричной системе, часто называют индийско-арабскими, потому что они происходят из Индии, откуда их позаимствовали арабы и позже усовершенствовали.
Самые ранние индийские цифры больше всего напоминают символы древних египтян. Например, в текстах кхароштхи, датируемых 400 г. до н. э. – 100 г. н. э., встречаются такие обозначения чисел от 1 до 8:
| || ||| X |X ||X |||X XX
с особым символом для 10. Первые признаки того, что постепенно приняло вид современной системы чисел, обнаружены в текстах брахми, датируемых примерно 300 г. до н. э. В буддийских текстах того времени найдены прообразы позднейших индийских символов для 1, 4 и 6. Но в системе брахми использовались разные символы для умножения на 10 и на 100, т. е. она оказалась ближе к греческой символике. Разница в том, что здесь предпочтение отдавалось символам, а не буквам алфавита. Брахми не была позиционной системой. К 100 г. н. э. сформировалась ее полная запись. Изображения в пещерах и на монетах доказывают, что ею продолжали пользоваться до IV в. н. э.
В IV–VI вв. на большую часть Индии распространилась власть империи Гуптов, и система чисел брахми преобразуется в систему гупта. Затем ее преобразуют в систему нагари. Суть оставалась прежней, менялись лишь символы.
Возможно, индусы изобрели позиционную систему еще в I в. н. э., но первые достоверные свидетельства использования такой записи чисел относятся к 594 г. Существует официальный документ, датированный 346 г. по календарю Чеди, но ряд ученых считают эту дату поддельной. Однако есть общее мнение, что позиционную систему в Индии стали использовать около 400 г. н. э.
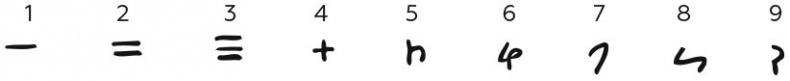
Цифры в системе брахми
Однако, поскольку символов было всего девять, от 1 до 9, возникала проблема двусмысленности обозначения. Например, что значит 25? Это может (в нашей системе) значить 25, или 205, или 2005, или 250 и т. д. В позиционной системе, где значение цифры зависит еще и от ее места, очень важно определить положение так, чтобы избежать двусмысленности. Сегодня мы добиваемся этого, используя десятый символ – ноль (0). А у древних цивилизаций ушло немало времени на то, чтобы выявить проблему и решить ее таким путем. Одной из причин была философская: как может ноль быть цифрой, если цифра обозначает количество предметов? Разве ничто можно сосчитать? Другая – практическая: обычно из контекста и так было ясно, что 25 означает именно 25, или 250, или что-то еще.
Незадолго до 400 г. до н. э. – точную дату установить невозможно – вавилоняне ввели специальный символ, чтобы показать пропущенную позицию в обозначениях цифр. Это освободило писцов от необходимости тратить силы на то, чтобы оставлять тщательно выверенное пустое место, и позволило легко и без ошибок определять число даже в случае, если оно было записано небрежно. Но об этом изобретении почему-то забыли (или оно не дошло до поздних культур), пока его заново не открыли индусы. Манускрипт Бакшали, дата написания которого пока точно не установлена, относят к периоду примерно между 200 и 1100 гг. н. э. Он содержит жирную точку. Джайнистский текст Локавибхаага 458 г. использует идею нуля, но не символ. Позиционная система, всё еще без нуля, представлена Арьябхатой в 500 г. н. э. В дальнейшем индийские математики также использовали понятие «ноль», но не символ. Первое бесспорное использование нуля в позиционной системе, датированное 876 г. н. э., появляется на каменных скрижалях Гвалиора.
Самыми выдающимися математиками Древней Индии считают Арьябхату (род. 476), Брахмагупту (род. 598), Махавиру (XI в.) и Бхаскару II (род. 1114). Формально их следовало бы причислить к астрономам, поскольку в то время математика считалась одной из астрономических техник. Их математические выкладки были разбросаны в отдельных главах в трудах по астрономии: никто не придавал им статуса самостоятельной науки.
Арьябхата утверждал, что свой труд «Арьябхатия» он создал в 23 года. Несмотря на краткость изложения, посвященный математике раздел его книги напичкан сведениями: буквенная система записи чисел, правила арифметики, методы решения простых и квадратных уравнений, тригонометрия (включая функции синуса и «обращенного синуса» 1 – cos θ). Также ему принадлежит превосходное по точности приближение 3,1416 для числа π.
Брахмагупта – автор двух книг: «Брахма-спхута-сиддханта» и «Кханда-кхадьяка». Первая – самая важная: это астрономический текст с углублением в математику, с арифметическими и словесными эквивалентами простой алгебры. Вторая книга в числе прочего включает замечательную интерполяционную формулу для вычисления синусов на основе небольшого числа известных табулированных значений этой функции: используются значения большего и меньшего углов, чем искомый.
Махавира исповедовал джайнизм и включил много положений этой религии в свой труд по математике, «Ганита-сара-самграха». Эта книга во многом повторяет труды Арьябхаты и Брахмагупты, но идет гораздо дальше и в целом намного сложнее. Она содержит описание дробей, перестановок и комбинаций, решение квадратных уравнений, теорему Пифагора и попытку вычислить периметр эллипса.
Бхаскара (известный также как «учитель») написал три известных труда: «Лилавати», «Биждаганита» и «Сиддханта-широмани» («Венец учения»). Согласно Фейзи, придворному поэту при могольском императоре Акбаре, дочь Бхаскары звали Лилавати. Отец решил составить ей гороскоп и вычислить точное время ее свадьбы. Чтобы придать своим манипуляциям наибольшую эффектность, он поместил дырявую чашку в таз с водой, так что в самый ответственный момент она должна была погрузиться на дно. Но Лилавати так низко наклонилась над водой, что жемчужинка с ее расшитого бусами платья отскочила и упала в чашку, закупорив дырку. Чашка так и не утонула, а это означало, что день свадьбы Лилавати никогда не наступит. Чтобы утешить дочь в ее горе, Бхаскара написал для нее труд по математике. Правда, легенда не уточняет, что подумала об этом сама девушка.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии