Магия математики. Как найти x и зачем это нужно - Артур Бенджамин Страница 12
Магия математики. Как найти x и зачем это нужно - Артур Бенджамин читать онлайн бесплатно
Ознакомительный фрагмент
x² + 4x + 4 = 16
Сделать это нужно для того, чтобы преобразовать левую часть в (x + 2)(x + 2). Так наша задачка превращается в
(x + 2)² = 16
Другими словами, (x + 2)² = 42. Значит,
x + 2 = 4 или x + 2 = –4
что дает нам x = 2 или x = –6, как мы уже выяснили чуть выше.
Но для уравнения
x² + 9x + 13 = 0
наш выбор очевиден – и это формула корней. У нас получается, что a = 1, b = 9, а c = 13. То есть
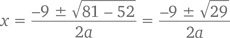
Согласитесь – в общем-то, не самый очевидный случай. По большому счету, в математике очень немного формул, которые действительно надо помнить, но формула корней квадратного уравнения – одна из них. Достаточно немного попрактиковаться, и вы легко обнаружите, что использовать эту формулу просто, как… дважды два.
Отступление
Почему работает формула корней квадратного уравнения? Давайте запишем уравнение ax² + bx + c = 0 как
ax² + bx= –c
а потом разделим обе части на a (которое не равно 0), чтобы получить
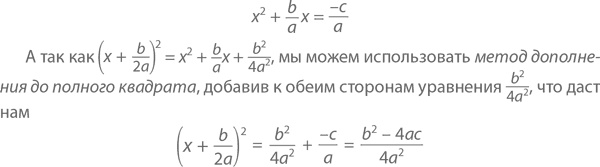
Извлечем квадратный корень из левой и правой частей уравнения:
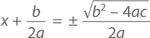
и в результате получим
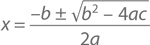
Что и требовалось доказать.
В XVII веке в математике произошел настоящий прорыв: французы Пьер де Ферма и Рене Декарт независимо друг от друга придумали отличный способ визуализации алгебраических уравнений (равно как и алгебраическую запись геометрических объектов).
Начнем, пожалуй, с графика простого уравнения
y = 2x + 3
Оно означает, что любое значение переменной х мы должны удвоить, а потом прибавить к нему 3 – так у нас и получается y. В таблице ниже приведены несколько возможных пар значений для x и y. Рядом с таблицей – график, на котором все эти значения отмечены точками, и можно легко видеть, что все они определенным образом упорядочены. Посмотрите на координаты: (–3, 3), (–2, –1), (–1, 1) и так далее. Соединив эти точки одной линией и уведя ее в бесконечность, мы получим то, что называется графиком. График рядом с таблицей есть отображение уравнения y = 2x + 3.
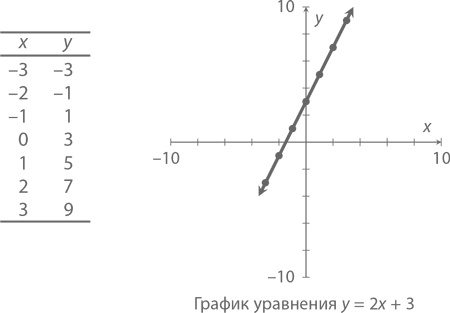
Добавим немного необходимой терминологии. Горизонтальная линия на нашей картинке называется осью X, вертикальная – осью Y. Сам график составляет линия с наклоном 2, которая пересекает ось Y в точке 3. Наклон – это степень «крутизны» линии. Наклон, равный 2, обозначает, что каждый раз, когда x увеличивается на одну единицу, y всегда будет увеличиваться на две (что очень хорошо видно из таблицы). Алгебраически точка пересечения с осью Y – значение y при x = 0. Геометрически же все очевидно: это точка пересечения графика с вертикальной линией. То есть график уравнения
y = mx+ b
представляет собой линию с наклоном m, которая пересекается с осью Y в точке b (и наоборот). Линия обычно ассоциируется с ее уравнением, Поэтому мы можем просто сказать, что график на предыдущем рисунке – это линия y = 2x + 3.
А вот график линий y = 2x – 2 и y = –x + 7:
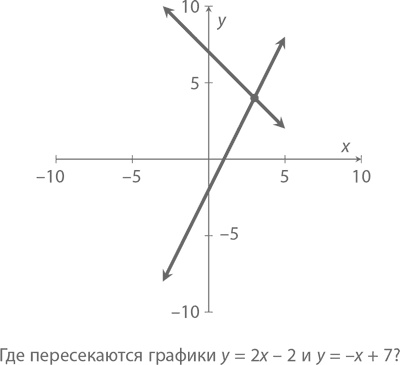
Первая линия y = 2x – 2 имеет наклон 2 и пересекается с осью Y в точке –2 (график получается параллельным линии y = 2x + 3 с полным сдвигом вниз по вертикали на 5). Наклон второй линии y = –x + 7 равен –1, поэтому при увеличении x на единицу на ту же единицу уменьшается и y. Призовем на помощь алгебру, чтобы найти точку (x, y) пересечения этих двух линий – именно в ней значения наших двух переменных совпадут, и x мы будем искать исходя из того, что он здесь равен y. Иными словами, нам надо решить
2x – 2 = –x + 7
Добавим к обеим частям сначала x, потом 2 и получим
3x = 9
то есть x = 3. А зная x, мы можем использовать другое уравнение, чтобы найти y. Если y = 2x – 2, значит, y = 2(3) – 2 = 4 (а y = –x + 7 дает нам y = –3 + 7 = 4). Значит, графики пересекаются в точке (3, 4).
Зная две точки, лежащие на одной прямой, нарисовать график в виде целой линии становится делом техники. Немного сложнее иметь дело с квадратичной функцией (и фигурирующим в ней x²). Самое простое для отображения в виде графика – уравнение y = x² (изображен ниже). Подобные графики называются параболами.
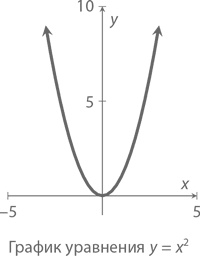
А вот график уравнения y = x² + 4x – 12 = (x + 6)(x – 2).
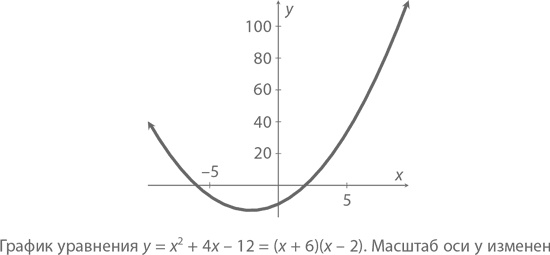
Обратите внимание, что, когда x = –6 или x = 2, y = 0. Это легко заметить на графике – в тех двух его местах, где парабола пересекает ось x. И совсем не случайно, что самая нижняя ее точка располагается точно в центре между ними – при x = –2 и y = –16. Это вершина.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии