Неопределенный электрический объект. Ампер. Классическая электродинамика. - Эугенио Мануэль Фернандес Агиляр Страница 11
Неопределенный электрический объект. Ампер. Классическая электродинамика. - Эугенио Мануэль Фернандес Агиляр читать онлайн бесплатно
f(x)=f(a) + f'(a)/1!(х - а)+f"(a)/2!(х - а)2+...+f(n)(a)/n!(х - а)n + Rn(f).
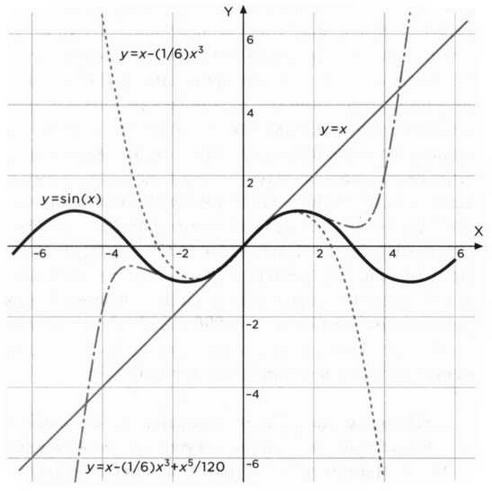
Разные линии отображают приближения 1, 3 и 5-й степени. Естественно, приближение 5-й степени лучше описывает функцию в точке 0.
В начале XIX века уравнения в частных производных (также называемые уравнениями в частных дифференциалах) вызывали большой интерес. Их изучение было связано с некоторыми проблемами физики — в частности, с волновыми уравнениями и уравнениями распространения тепла. При этом имена Лапласа, Коши, Пуассона и Фурье знакомы студентам физических и инженерных факультетов, однако вряд ли они слышали имя Ампера в связи с этими научными дисциплинами. Дело в том, что Ампер больше занимался классификацией уравнений, нежели решением конкретных физических проблем. Его система классификации уравнений в частных производных была хорошо принята, однако ее быстро превзошла система немецкого математика Поля Давида Густава Дюбуа-Реймона (1831-1889), и даже современные математики используют его терминологию. Превосходство системы немецкого математика объясняется очевидными пробелами в работе Ампера. Определения, предложенные французским ученым, неточны, обозначения сложны, теоремы не выстроены по степени важности, а примеры не развернуты. И все же оригинальность работы Ампера была замечена научным сообществом, и ему в 1815 году предложили стать членом Французской академии наук. Работы Ампера были высоко оценены и шотландским математиком Эндрю Расселом Форсайтом (1858-1942), известным среди историков науки благодаря своим многочисленным трактатам. В прекрасном девятитомнике под названием «Теория дифференциальных уравнений» (1890-1906) Форсайт неоднократно упоминает Ампера и положительно оценивает его вклад в изучение дифференциальных уравнений:
«Метод Ампера для интегрирования уравнений в частных производных представлен в двух выдающихся сообщениях во Французском Институте в 1814 году. Приложение метода к уравнениям первого порядка сегодня малоактуально по причине открытия других методов обращения с указанными уравнениями. Приложение же этого метода к уравнениям второго порядка необыкновенно важно. Доклады кажутся сложнее, чем они есть на самом деле, главным образом по причине сложности обозначений».
Ампер начинает свой доклад об уравнениях в частных производных, заменяя переменные, содержащие производные, заданные функцией z(x, у). Обозначим p = ∂z/∂x и q = ∂z/∂y, а вторые производные — r = ∂2z/∂x2, s = ∂2z/∂x∂y, t=∂2z/∂y2; явная функция выражается следующим образом:ƒ(х, у, z,p, q, r, s, t) = 0. Из этого Ампер выводит классификацию уравнений в частных производных, и на этом уровне проявляются неточности. Затем Ампер касается вопроса произвольных решений, который может возникать при рассмотрении уравнения в частных производных, и здесь начинается самая интересная часть доклада, в которой Ампер показывает, что уравнение в частных производных порядка т имеет общее решение, состоящее из по крайней мере т произвольных функций.
УРАВНЕНИЕ МОНЖА — АМПЕРА
В 1820 году, снова в Политехнической школе, Ампер опубликовал вторую работу об уравнениях в частных производных под названием «Приложение теории интегралов к уравнениям в частных производных первого и второго порядка». Если в работе 1815 года не хватало конкретных примеров, то новая работа была очень подробной, и в ней использовались новые знания. Здесь стоит упомянуть об уравнении, известном сегодня как уравнение Монжа — Ампера, которое записывается следующим образом:
Hr + 2Ks + Lt + M + N(rt-s2) = 0,
где H, К, L, M, N являются функциями первого порядка х, у, z, p и q. Первым к такому уравнению обратился французский математик Гаспар Монж (1746-1818), основатель современной описательной геометрии, хотя Ампер обобщил это уравнение и нашел его решения для конкретных случаев, без прямого приложения к физике. Однако последний пример касается волнового уравнения в упругой среде, которое Ампер решил, используя метод французского физика и математика Симеона Дени Пуассона (1781-1840). Этот пример показывает, что Ампер был знаком с математическими исследованиями того времени о дифференциальных уравнениях, несмотря на свой интерес к чистой математике. Ампер интересовался и геометрией. Об этом свидетельствует его статья 1808 года «О пользе для теории кривых линий, извлекаемой из рассмотрения соприкасающихся парабол».
ВСТУПЛЕНИЕ В ИНСТИТУТ ФРАНЦИИ И РАБОТА В ПОЛИТЕХНИЧЕСКОЙ ШКОЛЕ
В своих письмах и других рукописных документах Ампер упоминает Институт и Академию, не делая между ними различия. Однако разница между этими учреждениями есть, и стоит ее объяснить. Институт Франции был создан в 1795 году Конституцией III года, при Директории, с целью уничтожить королевские академии. До 1816 года Институт был разделен на «классы», однако затем Людовик XVIII решил вернуть для определения этих четырех классов название «Академия». Так появились Академия наук, Французская Академия, Академия надписей и изящной словесности и Академия изящных искусств. В 1832 году Луи-Филипп восстановил Академию моральных и политических наук, закрытую в 1795 году. Вступление в академию означало вступление в Институт, этим и объясняется взаимозаменяемость названий.
Некоторые биографы утверждают, что работа Ампера в Париже преследовала единственную цель — стать членом Академии наук, после чего ученый потерял к исследованиям всяческий интерес. Он действительно получил признание как математик в первые 15 лет пребывания в Париже, а его наиболее значительные работы были опубликованы между 1806 и 1820 годом. Именно в этот период Ампер доказал свой математический талант, что позволило ему стать членом Института в 1814 году. После этого ученый перестал регулярно публиковать работы, однако он все же представил несколько трудов о вариационном исчислении, дифференциальных уравнениях и разложении Тейлора.

Ампер в 1820 году.

Исследования Гаспара Монжа, графа де Пел юз, были важной основой для работ Ампера в области электричества и магнетизма.

Франц Антон Месмер, основатель месмеризма.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии