Как работает вселенная. Введение в современную космологию - Сергей Парновский Страница 11
Как работает вселенная. Введение в современную космологию - Сергей Парновский читать онлайн бесплатно
Ознакомительный фрагмент
Второй подход рассматривает красное смещение как результат эффекта Доплера, вызванного тем, что излучающий объект отдаляется от нас со скоростью его «разбегания». Для скоростей, существенно меньших скорости света с, т. е. при малых красных смещениях z << 1, его значение может быть приближенно записано как v = cz.
Скорость удаления объектов переводится в расстояния до них, используя закон Хаббла. Из-за неопределенности в значении параметра Хаббла расстояние часто выражается через безразмерную величину h = H0/(100 (км/с)/Мпк). Таким образом, скорость расширения 10 000 км/с переводится в расстояние 100 h–1 Мпк, иногда сокращается до 100 Мпк/h. Причина в том, что точность измерения z-фактора значительно выше, чем у параметра Хаббла, а расстояния, написанные таким образом, не теряют свою актуальность даже после изменения значения параметра Хаббла.
Мы еще раз подчеркиваем, что написанное выше – это не два разных эффекта, а два разных объяснения одного и того же эффекта. Их не надо объединять вместе.
Обратите внимание, что нехаббловские потоки также вызывают красное смещение, но только из-за вызванного скоростями их движения эффекта Доплера. Когда галактика движется в сторону близкой области с повышенной плотностью материи, это не сопровождается расширением пространства. Спектр ближайших галактик иногда смещен в фиолетовую область, что означает, что они движутся по направлению к нам. Этот эффект не имеет ничего общего с расширением Вселенной и обусловлен взаимным притяжением соседних галактик, например Млечного Пути и Андромеды. Поэтому астрономы не используют лучевые скорости для определения расстояния до близких объектов, но для далеких объектов это является основным методом измерения расстояний до них.
В этом разделе мы выводим закон Хаббла, предположив изотропию и однородность Вселенной.
Рассмотрим точки 1, 2 и 3 где-то во Вселенной, образующие треугольник, как показано на рис. 2.1. Длины сторон треугольника являются r21, r31 и r32. Длина r31 зависит не только от длины двух других сторон, но и от угла между ними. Изменяя угол, мы можем получить любое значение r31 в диапазоне от |r21 – r32 | до r21 + r32.
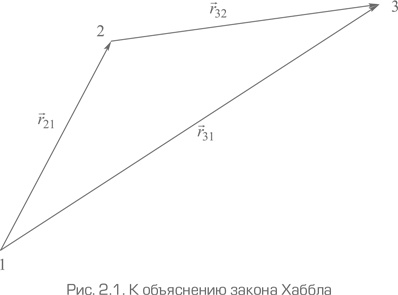
Из-за космологического расширения точки удаляются друг от друга. Рассмотрим движение частиц в двух других точках, наблюдаемых из определенной точки: скажем, из точки 1. Каждая из точек 2 и 3 может смещаться только в радиальном направлении от точки 1, в противном случае Вселенная была бы анизотропной. В изотропной Вселенной попросту нет никаких выделенных направлений, за исключением радиального. Скорости удаления всех частиц на расстоянии r от наблюдателя должны быть одинаковыми независимо от их направления, в противном случае Вселенная тоже была бы анизотропной. Таким образом, условие изотропии фиксирует скорость расширения в виде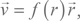
где f (r) – некоторая пока неизвестная функция.
Скорость точки 2 по отношению к наблюдателю в точке 1 равна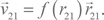
Точка 3 движется со скоростью
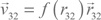относительно точки 2. Сложив эти скорости, мы получаем, что точка 3 движется со скоростью
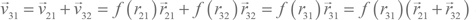относительно точки 1. Это дает нам условие:
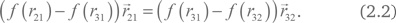
Так как векторы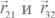
могут иметь разные направления, это возможно, только если
f (r21) = f (r31) = f (r32) = const. (2.3)
Таким образом, функция f (r) сводится к постоянной, которую мы называем постоянной Хаббла H. Следовательно, в однородной и изотропной Вселенной в любой момент времени единственно возможным законом расширения является закон Хаббла (2.1).
Обратите внимание, что при выводе закона Хаббла мы игнорировали релятивистские эффекты, связанные с конечностью скорости света. В релятивистском случае мы больше не можем просто складывать скорости, формулы становятся более сложными.
Выведем их. Согласно СТО, если тело движется со скоростью v относительно неподвижного наблюдателя, а второе тело движется в том же направлении со скоростью w относительно первого, то скорость второго тела относительно неподвижного наблюдателя равна:
Используя обратные гиперболические функции, это уравнение можно переписать в виде:
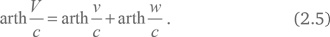
Гиперболический арктангенс может быть сведен к натуральным логарифмам как
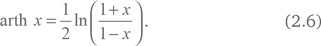
Если бы постоянная Хаббла H была действительно постоянной, то мы должны были бы использовать функцию c×arth (v/c) вместо v в законе Хаббла (2.1) и получить (здесь буквы th обозначают гиперболический тангенс):
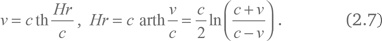
Тем не менее для скоростей намного меньше скорости света закон Хаббла в виде (2.1) хорошо работает.
Обратите внимание, что скорость v разбегания галактик и других космических объектов не может достичь скорости света с, и это никак не противоречит СТО. Расстояние r = c/H, таким образом, не является границей наблюдаемой части Вселенной, как многие ошибочно полагают. В разделе 3.4 мы обсудим космологический горизонт, который является настоящей границей видимой части Вселенной, но существование этой границы вызвано совершенно другой причиной.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.
Комментарии