Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления - Алекс Беллос Страница 11
Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления - Алекс Беллос читать онлайн бесплатно
Ознакомительный фрагмент
Попробуйте по этим правилам совершить «путешествие во времени», превратив сначала МИГ в ЧАС, затем ЧАС в ГОД, ГОД в ВЕК и наконец ВЕК в слово ЭРА. Всего эта цепочка занимает 17 ходов. А теперь постарайтесь сделать «скачок во времени» и превратить слово МИГ в ЭРА за шесть ходов.
8. Существует система присваивания числовых значений именам. В ней Дмитрий имеет значение 10, Василиса – 20, Петр и Глеб – по 5, а Ольга – 10. Какое значение в этой же системе у имени Дженнифер?
9. Какая буква завершает эту последовательность?
О Т Р Е Я У
10. Бессмыслица. При создании таких заданий берется любое крылатое выражение и все слова в нем заменяются на их научные (или вроде того) определения. В результате получается бессмыслица. Ваша задача – отгадать начальный вариант. Предлагаем решить две такие задачки [16].
1) Условием выживания биологической особи является ее перемещение по криволинейной замкнутой траектории.
2) Торговля мелкими домашними животными, расфасованными в непрозрачную тару, изготовленную из прочной материи.
Греческий математик Евклид, написавший книгу «Начала» примерно в 300 году до нашей эры, первым наглядно показал, какое удовольствие приносит логическая дедукция.
Несмотря на то что в «Началах» речь идет о геометрии, то есть о поведении точек, линий, поверхностей и тел, истинная значимость этого труда для истории человеческой мысли состоит в методе, введенном Евклидом для изучения этих концепций. Книга начинается с ряда определений, а пять сформулированных в ней основных правил можно принять в качестве постулатов. На основании исходных предпосылок Евклид делает все остальные выводы в «Началах» и на каждом этапе строго доказывает, как каждый очередной шаг вытекает из предыдущего. Сила этого метода – в стройной системе знаний, в которой истинность нескольких исходных утверждений гарантирует истинность выводов. Впоследствии на евклидову модель, описанную в «Началах», стала полагаться вся математика.
С практической точки зрения Евклид начинал с линейки и циркуля для построения линий и окружностей. Вот и все его инструменты. Каждая теорема в «Началах» – а их там сотни – доказана исключительно с их помощью.
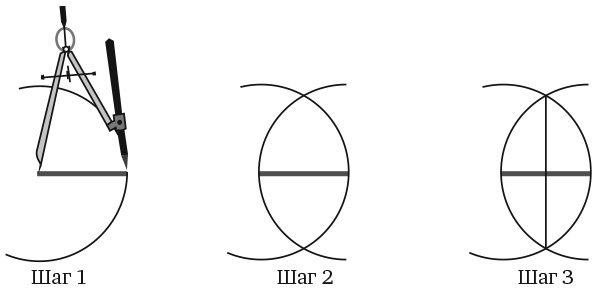
Например, как разделить отрезок пополам?
Шаг 1. Установите ножку циркуля с иглой в одной конечной точке отрезка, а ножку с карандашом – в другой конечной точке отрезка и нарисуйте окружность.
Шаг 2. Сделайте то же самое, установив ножку циркуля с иглой в другой конечной точке отрезка.
Шаг 3. С помощью линейки проведите прямую линию между точками пересечения окружностей.
Каждая теорема в «Началах» представлена в виде задачи, а каждое доказательство – в виде решения. По существу, это книга головоломок – во всем, кроме названия. В следующей головоломке мне нравится то, что она словно дразнит Евклида, мастера концептуальной бережливости, за то, что в его пенале слишком много инструментов.
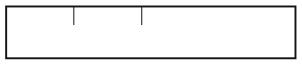
26. ТОЛЬКО ЛИНЕЙКА
У вас есть только карандаш и линейка. Как показано на рисунке, на линейке всего две метки. Можете ли вы провести отрезок, длина которого равна половине расстояния между ними? Другими словами, если расстояние между двумя метками составляет 2 единицы, проведете ли вы отрезок длиной в 1 единицу?
Измерения разрешается выполнять только с помощью линейки, не используя карандаш и бумагу.
Все задачи в этой главе геометрические в том смысле, что они позволяют изучить свойства линий, фигур и объектов и получить при этом удовольствие. Следующая задача взята из издания «Начал» XVIII века с примечаниями британского ученого Уильяма Уистона, преемника Ньютона на должности лукасовского профессора математики [17] в Кембриджском университете. Уистон обратил внимание на одну математическую странность, положенную в основу известной головоломки.
Ученый вычислил, насколько большее расстояние проходит голова человека, огибающего земной шар по окружности, по сравнению с расстоянием, пройденным ногами. Можете ли вы подсчитать это дополнительное расстояние исходя из предположения, что земной шар имеет сферическую форму?
Я выполню для вас эти расчеты, но нам понадобятся некоторые элементарные математические знания, а именно формула длины окружности, равная произведению радиуса и двух π, которую обычно записывают как 2π, где π примерно равно 3,14. Надеюсь, ее введение не уведет вас в сторону от удивительного, неожиданного результата. Потерпите немного, пока я буду делать вычисления.
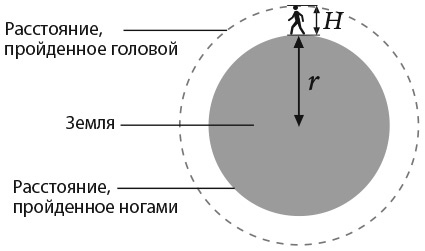
На рисунке r – это радиус Земли, а H – рост человека. По формуле длина окружности земного шара (расстояние, пройденное ногами человека) равна 2πr, а длина окружности, обозначенной пунктиром (расстояние, пройденное головой), составляет 2πr(r + H), поскольку радиус пунктирной окружности равен радиусу Земли плюс рост человека. Таким образом, разность между длинами двух окружностей, которая показывает, насколько большее расстояние проходит голова человека, составляет:
2πr(r + H) – 2πr = 2πr + 2πH – 2πr = 2πH.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии