Математическое мышление - Джо Боулер Страница 16

Чтобы успешно изучать язык и литературу, читать и понимать прозу или поэзию, необходимо запоминать значение множества слов. Но ни один ученик, изучающий язык и литературу, не скажет и не подумает, что весь процесс сводится к быстрому запоминанию слов и их восстановлению в памяти. Ведь мы изучаем слова, используя их во множестве разных ситуаций: когда разговариваем, читаем и пишем. Учителя-словесники не заставляют детей запоминать сотни лексических единиц и не проверяют их в условиях ограничений времени. Все дисциплины требуют запоминания тех или иных фактов, но математика — единственный предмет, преподаватели которого убеждены в необходимости тестов с ограничением времени. Почему так? У нас есть результаты исследований, подтверждающие, что ученики могут гораздо эффективнее усваивать математические факты в рамках увлекательных занятий; пора с их помощью избавить учеников от страха математики.

Насколько важна практика в математике?

Когда я предъявляю родителям и учителям доказательства того, что детям нужно заниматься математикой на концептуальном и визуальном уровнях, некоторые спрашивают: «Разве не нужно много практиковаться?» Под практикой при этом подразумеваются многие страницы отдельных заданий по математике. Нужна ли ученикам практика по математике и в каком виде — вопрос интересный. Мы знаем, что процесс обучения сопровождается возбуждением синапсов, а чтобы в мозге произошли структурные изменения, нужно не единожды рассматривать идеи и глубоко изучать их. Но что это значит? Математические концепции действительно важно рассматривать неоднократно, но снова и снова «отрабатывать» методы бесполезно. Когда вы изучаете новую концепцию, стоит закрепить ее, и лучший способ сделать это — использовать ее разными способами. Мы вредим ученикам, когда формулируем самый простой вариант концепции и даем 40 заданий, в которых используется только он. Листы с письменными заданиями, в которых многократно повторяется одна и та же концепция, отталкивают учеников от математики; в них нет нужды, поскольку они не учат применять концепцию в разных ситуациях.

В своем бестселлере «Гении и аутсайдеры»^[11] Малкольм Гладуэлл развивает идею о том, что для достижения высокого уровня мастерства в любой области нужны примерно 10 тысяч часов практики. Гладуэлл описывает достижения знаменитых музыкантов, шахматистов и спортсменов, отмечая при этом один важный момент. Многие считают, что такие люди, как Бетховен, гениальны от рождения. А Гладуэлл показывает, что они долго и упорно трудятся, чтобы добиться серьезных результатов, и обладают мышлением роста, которое помогает им в работе. К сожалению, многие люди, с которыми я беседовала, интерпретируют идею Гладуэлла так, будто ученики могут овладеть математикой на высоком уровне после 10 тысяч часов бездумной практики. Это неверно. Овладение математикой требует работы в истинном математическом смысле. Нам не нужно, чтобы ученики снова и снова отрабатывали один и тот же метод. Это не математика; такой подход не дает знания идей, концепций и взаимосвязей, позволяющего овладеть наукой на высоком уровне. В эти 10 тысяч часов необходимо изучать математику в целом, анализируя ее концепции и связи, решая задачи, делая умозаключения и связывая разные методы воедино.

Авторы большинства учебников в США используют стандартный подход, когда необходимо выделить методы, свести их к простейшей форме, а затем отрабатывать. Это создает ряд проблем. Во-первых, изучение отдельных методов вызывает скуку; многие дети теряют интерес к математике, когда им кажется, что их роль состоит в пассивном принятии конкретного метода (Boaler & Greeno, 2000) и его многократном повторении. Во-вторых, в большинстве практических заданий показан самый простой и обособленный вариант метода, поэтому ученики не имеют ни малейшего представления о том, когда и как еще они могут применить его.

Примеры концепций в учебниках тоже не показательны: составители пособий всегда выбирают самый простой вариант. В примере 4.1 приведены ответы учеников на математические вопросы в ходе научных исследований, а также отмечен характер проблемы, вызванной традиционной постановкой вопросов в учебниках.

ПРИМЕР 4.1

Ученикам в возрасте 11 лет показали следующий рисунок и задали вопрос: прямая a параллельна прямой c?

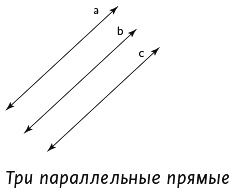
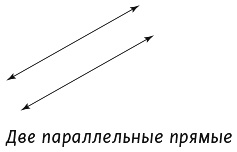
Большинство учеников дали ответ: «Нет, потому что между ними находится прямая b». Причина в том, что понятие параллельности почти всегда иллюстрируют рисунком с двумя прямыми.

Затем учеников попросили назвать следующую фигуру.

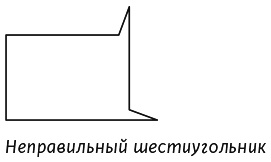
Большинство не смогли этого сделать. На рисунке изображен шестиугольник (многоугольник с шестью сторонами), но шестиугольники почти всегда показывают в таком виде.

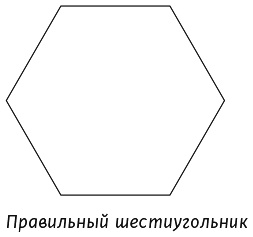
Это не отражает в полной мере концепцию шестиугольника.

Более половины учеников восьми лет не воспринимают представленные ниже фигуры как прямой угол, треугольник, квадрат и параллельные прямые…

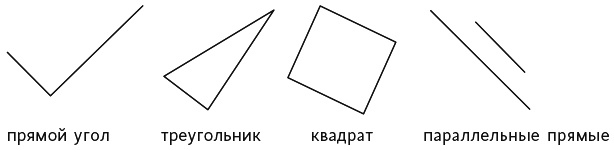
Незнакомые изображения геометрических концепций

…поскольку им всегда показывают самый простой вариант. Вот знакомые изображения, которые ученики ожидают увидеть.

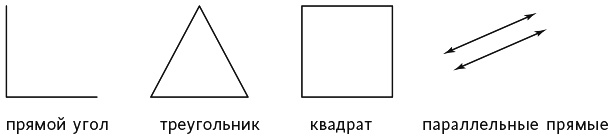
Знакомые изображения геометрических концепций

Итак, более половины учеников, принимавших участие в исследовании, не смогли правильно назвать фигуры. И вот что это значит: когда в учебниках приводится только самый простой вариант идеи, ученики не могут узнать, в чем состоит ее суть. Дети не смогли правильно опознать разные объекты, поскольку авторы учебников неизменно приводят «идеальные примеры». Когда ученики изучают какое-то понятие, вместо идеальных примеров целесообразно предлагать им разные, чтобы некоторые из них едва отвечали этому определению, а некоторые вообще не соответствовали ему.

Учителя математики должны также давать достаточно широкое определение той концепции, которую изучают ученики, и иногда это лучше всего сделать с помощью правдоподобных, но ложных примеров. В процессе изучения определения часто полезно приводить как примеры, отвечающие ему, так и не отвечающие ему, а не идеальные варианты. Например, когда ученики изучают птиц, стоит напомнить им о летучих мышах и предложить подумать, почему они не относятся к птицам, а не рассматривать все больше изображений воробьев, ворон и других птиц.