Математическое мышление - Джо Боулер Страница 10
Математическое мышление - Джо Боулер читать онлайн бесплатно
Ознакомительный фрагмент
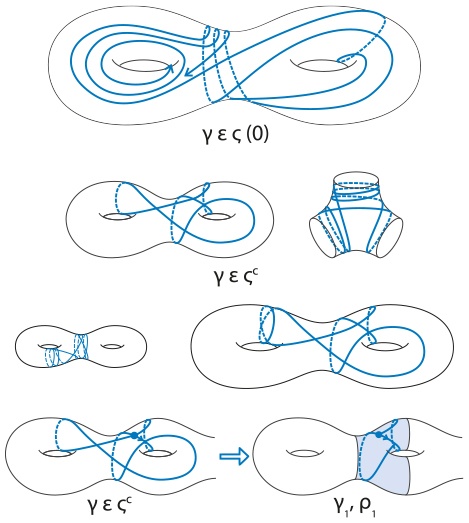
Рис. 3.1. Некоторые идеи из докторской диссертации Жени Сепир по математике
Публикуется с разрешения Жени Сепир.
Во время защиты диссертации профессора три или четыре раза задавали вопросы, на которые уверенная в себе молодая женщина отвечала: «Я не знаю». Часто профессор прибавлял, что он тоже не знает. Было необычно слышать «не знаю» на защите докторской диссертации. Некоторые профессора отнеслись бы к этому с неодобрением. Но истинная математика — дисциплина, которой свойственна неопределенность. Ее суть сводится к исследованиям, гипотезам и интерпретациям, а не однозначным ответам. Присутствовавшие на защите профессора сочли вполне обоснованным то, что Женя не знала ответов на некоторые вопросы, поскольку ее работа вступала в область неизведанного. Женя Сепир блестяще защитила диссертацию.
Все это не значит, что математика не дает ответов на вопросы. Многие математические факты известны, и ученикам важно изучить их. Однако по каким-то причинам школьная математика оказалась настолько далека от математики истинной, что если бы в тот день я привела школьников на защиту диссертации, то они не поняли бы, о чем речь. Именно большой разрыв между истинной математикой и школьным предметом стал основой проблем с этой дисциплиной в сфере образования. Я глубоко убеждена, что если бы во время школьных уроков математики учителя раскрывали истинную суть этого предмета, то не было бы ни всеобщей неприязни к нему, ни низкой успеваемости.
Математика — культурный феномен. Это совокупность идей, связей и соотношений, позволяющая человеку осмыслить мир. По сути, это наука о закономерностях. Если взглянуть на мир сквозь призму математики, можно найти закономерности повсюду. И их понимание, полученное в рамках изучения математики, обеспечивает создание новых, эффективных знаний. Выдающийся математик Кит Девлин посвятил книгу этой теме. В своей работе «Математика: наука о закономерностях» он пишет следующее.
Поскольку математика — наука об абстрактных закономерностях, практически не существует аспектов нашей жизни, на которые она не влияет. Ведь абстрактные закономерности определяют суть мышления, коммуникации, вычислений, общества и самой жизни (Devlin, 1997).
Знание математических закономерностей помогает людям покорять океаны, прокладывать маршруты космических полетов, разрабатывать технологии для мобильных телефонов и социальных сетей, а также создавать новые научные и медицинские знания. Однако многие ученики считают, что математика — мертвая наука, не имеющая отношения к их будущему.
Чтобы понять суть математики, следует рассмотреть ее закономерности в реальном мире. Закономерности в океане и дикой природе, архитектуре и осадках, поведении животных и социальных сетях вызывают у математиков восхищение. Последовательность Фибоначчи, пожалуй, самая известная из них. Фибоначчи — итальянский математик, опубликовавший в 1202 году в Италии работу о закономерности, названной в его честь. Сейчас известно, что она появилась несколькими столетиями ранее, еще в 200 году до н. э., в Индии. Вот как выглядит последовательность Фибоначчи:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
Первые два числа — 1 и 1, а каждое следующее представляет собой сумму двух предыдущих.
Попробуйте приглядеться к снежинкам. Каждая из них уникальна, но их объединяет одна закономерность. Все снежинки имеют шестиугольную структуру, поэтому у них всегда шесть концов (рис. 3.2 и 3.3).
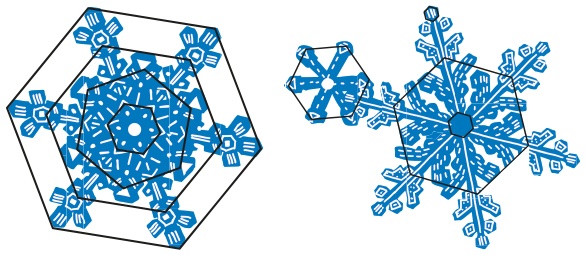
Рис. 3.2. Математика в снежинках
Рис. 3.3. Молекулы воды
Во время онлайн-курса для учеников, изучающих математику, в котором поучаствовало более 100 тысяч слушателей, я показала, как математику используют животные. Аудитория заинтересовалась этим. Например, дельфины находят друг друга в воде с помощью звуков (рис. 3.4).
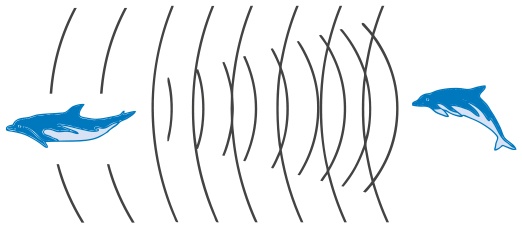
Рис. 3.4. Общение между дельфинами
Дельфин издает характерные щелкающие звуки, которые отражаются от различных объектов и возвращаются к нему. Затем по времени прохождения и характеристикам звукового сигнала животное определяет, где находятся его друзья. Он интуитивно вычисляет скорость, то есть находит ответ на тот самый вопрос о скорости, который задают ученикам на уроках алгебры (во многих случаях он никак не связан с реальной жизнью). Во время онлайн-курса я в шутку сказала слушателям, что, если бы дельфины могли разговаривать на человеческом языке, они стали бы учителями алгебры!
Во время исследований для онлайн-курса моя студентка Микаэла обнаружила, что пауки — настоящие эксперты по спиралям. Когда паук создает паутину, он сначала плетет фигуру в форме звезды между двумя прочными вертикальными опорами, например ветвями дерева. Затем паук закручивает спираль. Ему нужно построить ее как можно быстрее, чтобы закрепить звезду, поэтому он выбирает логарифмическую спираль. В ней расстояние между следующими друг за другом витками вокруг центра увеличивается в одинаковое количество раз (рис. 3.5).
Рис. 3.5. Паутина
Получается, чем больше спираль, тем быстрее она расширяется. Но при этом в паутине образуются большие промежутки, поэтому паук начинает строить еще одну, более плотную спираль, одновременно отцепляя первую. Новая спираль — арифметическая, в ней расстояние между витками постоянно. Плетение второй спирали занимает гораздо больше времени, поскольку приходится делать больше кругов вокруг центра звезды. Но это помогает пауку поймать больше насекомых, поскольку в сети не остается крупных промежутков. Такую поразительную инженерную конструкцию можно было бы построить с помощью вычислений, но паук интуитивно использует математику при разработке и применении своего алгоритма. Другие примеры использования математики животными можно найти в работах Кита Девлина (Devlin, 2006).
Когда я демонстрировала все эти идеи слушателям своего онлайн-курса, некоторые из них не соглашались со мной, заявляя, что математика в природе и мире животных — это не математика. Эти люди признавали только область чисел и вычислений. Я хотела подтолкнуть слушателей к более широкому восприятию предмета. И достигла своей цели. К концу курса среди слушателей был проведен опрос, в ходе которого 70% респондентов сказали, что изменили свои представления о том, что такое математика. При этом 75% слушателей убедили себя, что они могут добиться успеха в математике.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии