Истина и красота. Всемирная история симметрии - Йен Стюарт Страница 45
Истина и красота. Всемирная история симметрии - Йен Стюарт читать онлайн бесплатно
В 1882 году, на полпути между поездкой в Париж и своим назначением в Кенигсберг, Линдеманн понял, как распространить метод Эрмита на доказательство трансцендентности числа π. Именно это и принесло ему славу. Некоторые историки полагают, что Линдеманну просто повезло — что он просто случайно наткнулся на правильное обобщение блестящей идеи Эрмита. Но, как однажды заметил гольфист Гари Плеер, «чем лучше я играю, тем больше мне везет». Так же, по-видимому, обстояло дело и с Линдеманном. Если могло повезти кому-то, то почему не повезло Эрмиту? Позднее Линдеманн обратился к математической физике, занявшись исследованиями электрона. Наиболее известным из его учеников был Давид Гильберт.
Данное Линдеманном доказательство трансцендентности числа π опиралось на метод, впервые использованный Ламбертом и развитый Эрмитом: придумать подходящий интеграл, вычислить его двумя способами и показать, что если число π алгебраическое, то ответы не согласуются. Интеграл был очень тесно связан с тем, который использовал Эрмит, только еще более сложному. Связь между e и π выражалась в прекрасном соотношении, открытом Эйлером. Если бы π было алгебраическим, то e приобрело бы некоторые новые неожиданные свойства — похожие на свойства алгебраических чисел, но все же отличающиеся от них. Ядро доказательства Линдеманна относилось к числу e, а не к π.
С появлением доказательства Линдеманна эта глава математики пришла к своему первому действительно важному выводу. Невозможность квадратуры круга оказалась не более чем побочным эффектом. Гораздо важнее для математиков было понять, почему так происходит. Теперь они могли двигаться вперед и развивать теорию трансцендентных чисел, которая сегодня представляет собой активную (и дьявольски сложную) область исследований. Даже наиболее очевидные и на вид правдоподобные гипотезы о трансцендентных числах остаются по большей части недоказанными.
Вооруженные достижениями Абеля и Галуа, мы можем вернуться к задаче о построении правильных многоугольников. Для каких чисел n можно построить правильный n-угольник циркулем и линейкой? Ответ на этот вопрос весьма необычен.
В Disquisitiones Arithmeticae Гаусс сформулировал необходимые и достаточные условия на целое число n, но доказал только их достаточность. По его утверждению, у него было доказательство, что те же условия являются и необходимыми, но, как и большая часть его результатов, оно осталось неопубликованным. Гаусс в действительности выполнил сложную часть работы, а Ванцель привел недостающие подробности в своей статье 1837 года.
Чтобы лучше понять данный Гауссом ответ, рассмотрим правильный 17-угольник. Что есть такого в числе 17, что позволяет построить правильный многоугольник с 17 сторонами? Почему это невозможно, скажем, для чисел 11 или 13? Заметим, что все эти три числа — простые. Легко показать, что если правильный n-угольник допускает построение, то можно построить правильный p-угольник для каждого простого числа p, на которое делится n. Надо просто взять каждый n/p-угол. Например, если взять каждую третью вершину в правильном 15-угольнике, получим правильный 5-угольник. Так что имеет смысл рассматривать простое число сторон, а затем получить полное решение, используя результаты для простых чисел.
Число 17 простое, что для начала уже неплохо. Выполненный Гауссом анализ, переформулированный в более современных терминах, основан на том факте, что решения уравнения x17 − 1 = 0 образуют вершины правильного 17-угольника на комплексной плоскости. У этого уравнения имеется один очевидный корень x = 1. Остальные 16 — это корни многочлена 16-й степени, и можно показать, что этот многочлен есть x16 + x15 + x14 + … + x2 + x + 1. 17-угольник строится путем решения цепочки квадратных уравнений, а это оказывается возможным потому, что 16 есть степень числа 2: 16 = 24.
Аналогично в более общем случае аргументы того же типа показывают, что когда p — нечетное простое число, правильный p-угольник допускает построение, если и только если p − 1 есть степень числа 2. Такие нечетные простые числа называются (простыми) числами Ферма, потому что Ферма первым взялся их исследовать. Грекам было известно о построении правильного 3-угольника и правильного 5-угольника. Заметим, что 3 − 1 = 2 и 5 − 1 = 4 суть степени числа 2. Результаты греков, таким образом, согласуются с критерием Гаусса, а 3 и 5 — первые два из чисел Ферма. С другой стороны, 7 − 1 = 6, что не есть степень двойки, так что правильный 7-угольник не допускает построения циркулем и линейкой.
Затратив еще немного труда, можно получить характеризацию Гаусса: правильный n-угольник допускает построение, если, и только если, n является степенью двойки или же степенью двойки, умноженной на различные простые числа Ферма.
Остается выяснить, каковы же числа Ферма. Следующим после 3 и 5 идет Гауссово 17. Следующее — 257, а за ним — уже довольно большое число 65 537. Это единственные известные простые числа Ферма. Никто не доказал, что дальнейшие числа Ферма существуют — но никто не доказал и того, что их нет. Насколько нам известно на данный момент, может существовать абсолютно гигантское простое число Ферма, пока не известное человечеству. Согласно знаниям, имеющимся на сегодняшний день, это число составляет по меньшей мере 233554432 + 1, и этот монстр и в самом деле может оказаться следующим простым числом Ферма. (Показатель степени 33 554 432 сам есть степень числа 2, а именно 225. Все числа Ферма на единицу превосходят двойку, возведенную в степень, являющуюся степенью двойки.) Это число имеет более десяти миллионов знаков. Даже после сделанных Гауссом великих открытий мы все равно не знаем в точности, какие именно правильные многоугольники можно построить, но единственным пробелом в наших знаниях остается вопрос о существовании очень больших чисел Ферма.
Гаусс доказал, что правильный 17-угольник допускает построение, но в действительности не дал описания самого построения, хотя и заметил, что основной шаг состоит в построении отрезка, длина которого равна
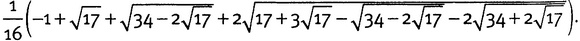
Поскольку квадратные корни можно построить всегда, искомое построение скрыто в этом замечательном числе. Первое явное построение осуществил Ульрих фон Югэнен в 1803 году. В 1893 году Герберт Уильям Ричмонд нашел более простой вариант [34].
В 1832 году Ф. Ж. Ришло опубликовал ряд статей о построении правильного 257-угольника под заголовком De resolutione algebraica aequationis x257 = 1, sive de divisione circuli per bisectionem anguli septies repetitam in partes 257 inter se aequales commentatio coronata, который сам уже производит не меньшее впечатление, чем число сторон его многоугольника.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии