Логика чудес. Осмысление событий редких, очень редких и редких до невозможности - Ласло Мерё Страница 10
Логика чудес. Осмысление событий редких, очень редких и редких до невозможности - Ласло Мерё читать онлайн бесплатно
Ознакомительный фрагмент
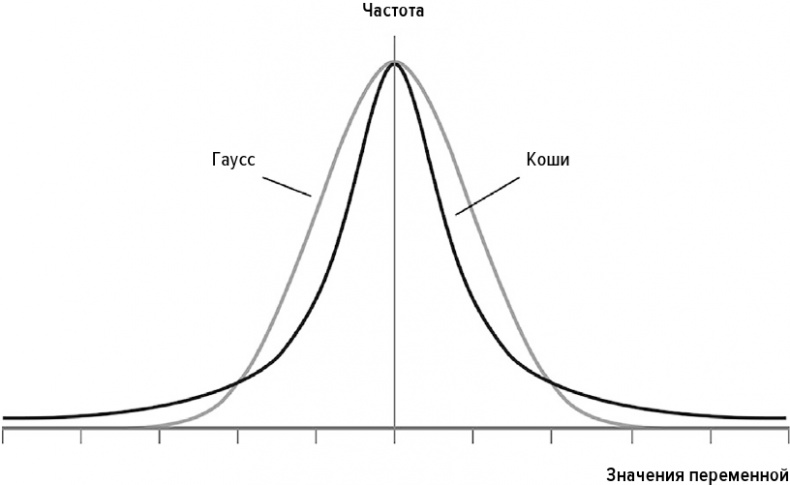
Илл. 5. Распределения Гаусса и Коши
(График Йожефа Бенце)
Математик сказал бы, что распределение Коши не имеет математического ожидания. Среднее значение по большому числу выстрелов может соответствовать любой точке стены. Именно этого не происходит в распределении Гаусса. Чем больше производится выстрелов, тем ближе среднее значение распределения Гаусса оказывается к середине стены, потому что очень редкие попадания в удаленные точки компенсируются гораздо бо́льшим числом попаданий в точки, расположенные ближе к центру.
Нет у распределения Коши и стандартного отклонения. При этом отсутствие у него стандартного отклонения отличается от его отсутствия у одного Эйнштейна. На самом деле было бы точнее сказать, что у Эйнштейна есть стандартное отклонение, но оно равно нулю и, следовательно, не поддается разумной интерпретации. Распределение Коши не имеет стандартного отклонения в том смысле, что не существует столь большого числа измерений, которое позволило бы определить типичное отклонение попаданий от середины. Во всех явлениях, которые хорошо моделируются распределением Коши, стандартного отклонения не имеет не только единственный и неповторимый Эйнштейн; оказывается, что его не имеет и все население.
Концепция Коши приводит к дикому миру, в котором нельзя даже говорить о таких «очевидных» вещах, как типичное отклонение от типичного значения, — потому что ничего такого не существует: ни типичного значения (математического ожидания), ни типичного отклонения. Невозможно сказать, что является «средним». Если вам нужно среднее, вам придется оставить мир Коши и вернуться в безопасный и тихий мир Гаусса.
Поэтому можно сказать, что математика Тихонии происходит от Гаусса, а математика Диконии — от Коши. То, что редкость в Гауссовой Тихонии, может быть делом сравнительно обычным в Диконии Коши — например, выстрелы, поражающие цель далеко за пределами нашего поля зрения. Если бы человеческий рост был распределен по Коши, время от времени появлялись бы люди, рост которых доходил бы до пяти, десяти и даже тысячи метров. Во всех остальных отношениях эти люди были бы такими же, как мы, но только выросшими по случаю чрезвычайно высокими — так же как Фиби по случаю стреляет почти параллельно стене. В части III этой книги мы увидим, как распределение Коши привело к открытию некоторых странных законов Диконии.
Я оставил без ответа вопрос о том, следует ли считать гения чудом или просто человеком необычайно талантливым. Сделан ли он (сделана ли она) из того же материала, что и любой другой одаренный индивидуум? Возвращаясь к нашей метафоре, является ли гений попросту проявлением выстрела, который Фиби делает почти параллельно стене? Когда мой друг Алекс сказал, что то, что кажется чудом мне, может не казаться таковым человеку, гораздо более талантливому, он мог бы добавить: «Поскольку ты находишься сравнительно близко к середине, ты видишь не очень далеко, но человек, оказавшийся на большем расстоянии от нее, может видеть дальше; возможно, такому человеку может быть видно, что гения создал тот же стрелок, который создал и всех нас».
Пока что Алекс вполне может оставаться при своих убеждениях. Ему будет приятно узнать, что открытие Диконии подкрепляет его точку зрения: существуют явления, которые кажутся обычному разуму чудесами, но могут быть объяснены законами Диконии. Идея Диконии приемлема для Алекса, потому что это чисто научная концепция. До сих пор он был знаком только с Тихонией и безоговорочно верил в ее законы, хотя, по-видимому, не настолько, чтобы это помешало ему попытаться вывести венгерскую компанию на биржу Nasdaq.
Открытие Диконии помогло нам понять, что в тех частях мира, которые управляются диконскими законами, следует ожидать, что время от времени будут возникать чрезвычайно сильные отклонения, противоречащие здравому смыслу. До этого, когда объяснения можно было почерпнуть только из законов Тихонии, такие события считались чудесами. Но в Диконии торжествует точка зрения Алекса: такие отклонения — не чудеса, и в будущем гарантированно будут возникать другие, даже еще более крупные.
Возможно, законы Диконии лучше описывают не только миры финансов и технологий, но и мир человеческих способностей. Если это так, то, возможно, Алекс снова прав, и гениальность может быть всего лишь экстремальным проявлением талантливости в Диконии. С другой стороны, наука не просто все глубже и глубже проникала в законы дикого мира. Она установила также, что всегда будут существовать такие явления, объяснение которых выходит за пределы наших современных знаний.
Идея о том, что природа не терпит пустоты, — это древний принцип натуральной философии, восходящий по меньшей мере к Аристотелю, который утверждал, что, если попытаться удалить из некоторой области пространства всю материю, окружающая материя стремительно заполнит образовавшийся вакуум. Действительно, в нашем повседневном опыте природа рано или поздно заполняет все пустоты, по меньшей мере здесь, на Земле, где сила тяжести тянет все объекты вниз. В космическом пространстве, в котором вакуум — не исключение, а правило, дело обстоит совсем иначе. Тем не менее существуют признаки того, что нетерпимость к пустоте в той или иной форме и правда проявляется в весьма широкой области. По аналогии можно сказать, что всюду, где имеется пробел в знаниях — нечто, чего наука не может объяснить, — эта пустота неизбежно заполняется, как правило, объяснением, которое называет такое явление чудом.
Но, возможно, некоторые вещи будут считаться чудесами всегда, как бы далеко ни продвинулась наука. Я предлагаю отнести к этой категории появление гения, который, судя по многочисленным свидетельствам, во многих отношениях совершенно отличается от остальных людей. В терминах предложенной нами выше метафоры гений, возможно, аналогичен не случаю, в котором Фиби стреляет почти параллельно стене, а чему-то, вовсе не имеющему отношения к стрельбе. В таком случае гений — не удаленное от середины пулевое отверстие, но нечто принципиально иное, даже если во всех остальных отношениях гений выглядит точно так же, как и все остальные пулевые отверстия. Но если гений — всего лишь человек из плоти и крови, подобный всем остальным людям, как же гениальность может принципиально отличаться от талантливости? Я отвечу на этот вопрос и проясню введенные здесь смутные идеи в следующей главе, после разговора о «гипервещественных» числах.
Именно потому, что гений настолько сильно отличается от остальных людей, порог гениальности устанавливается так высоко. Даже Гаусса, возможно, следует считать всего лишь человеком чрезвычайно талантливым. Например, одна из его великих идей, возможность существования неевклидовой геометрии, которую он не счел достойной развития и публикации, была независимо разработана венгерским математиком Яношем Бойяи и российским ученым Николаем Ивановичем Лобачевским. Это говорит о том, что, хотя Гаусс обладал необычайным талантом, он не выдвигал идей, которых не мог вообразить никто другой. С другой стороны, Ньютон и Эйнштейн предложили новые космологии, никогда не приходившие в голову другим великим ученым и изменившие наши представления о Вселенной.
Жалоба
Напишите нам, и мы в срочном порядке примем меры.





Комментарии